Trọng tâm của tam giác là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học phẳng, giúp chúng ta hiểu rõ hơn về cấu trúc và các đặc điểm của tam giác. Để nắm vững kiến thức này, hãy cùng tìm hiểu Trọng Tâm Của Tam Giác Là Gì qua định nghĩa, các tính chất nổi bật cùng ví dụ minh họa cụ thể dưới đây.
I. Định Nghĩa Trọng Tâm Của Tam Giác
Trọng tâm của tam giác được định nghĩa là giao điểm của ba đường trung tuyến trong tam giác đó. Mỗi đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.
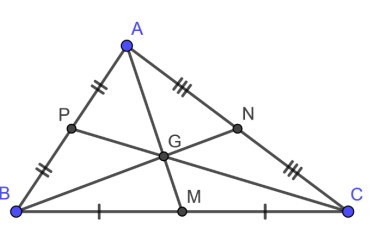Minh họa các đường trung tuyến và trọng tâm của tam giác ABC
Cụ thể, trong tam giác ABC, nếu AM, BN, và CP là ba đường trung tuyến (với M, N, P lần lượt là trung điểm của BC, AC, AB), thì ba đường này sẽ cùng đi qua một điểm duy nhất, điểm đó được gọi là trọng tâm tam giác ABC. Điểm này có vai trò đặc biệt, giống như việc hiểu trọng tâm của tam giác đều sẽ mang lại cái nhìn sâu sắc hơn về tính đối xứng.
II. Tính Chất Nổi Bật Của Trọng Tâm Tam Giác
Trọng tâm của tam giác mang một tính chất đặc trưng và quan trọng: trọng tâm cách mỗi đỉnh một khoảng bằng hai phần ba (2/3) độ dài đường trung tuyến đi qua đỉnh ấy.
Giả sử G là trọng tâm của tam giác ABC và AM, BN, CP là các đường trung tuyến tương ứng. Khi đó, ta có các mối quan hệ về độ dài sau:
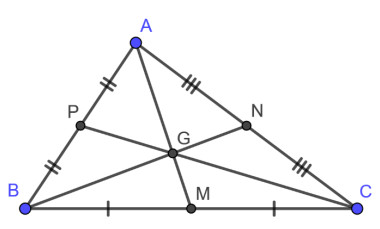Mô tả trọng tâm G chia đường trung tuyến theo tỷ lệ 2:1
- AG = (2/3) AM
- BG = (2/3) BN
- CG = (2/3) CP
Đồng thời, chúng ta cũng suy ra được các tỷ lệ khác: GM = (1/3) AM, GN = (1/3) BN, GP = (1/3) CP. Từ đó, AG = 2GM, BG = 2GN, CG = 2GP. Việc nắm vững các mối quan hệ này rất hữu ích, tương tự như khi tìm hiểu về đường cao trong tam giác vuông để giải quyết các bài toán hình học phức tạp. Mặc dù khái niệm “tâm” có nhiều ý nghĩa, như trong câu nói tâm sinh tướng là gì, trong hình học, trọng tâm chỉ về một vị trí cố định.
III. Ví Dụ Minh Họa
Để hiểu rõ hơn về cách áp dụng tính chất của trọng tâm, hãy xem xét ví dụ sau:
Ví dụ: Cho tam giác ABC có trọng tâm G. Biết AM là đường trung tuyến với M thuộc cạnh BC và AM = 12cm. Tính độ dài đoạn AG và GM?
Hướng dẫn:
Vì G là trọng tâm tam giác ABC, theo tính chất của trọng tâm, ta có:
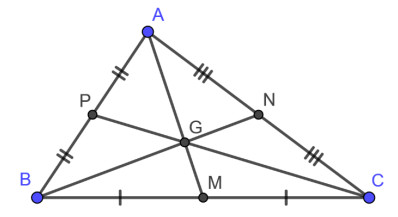Ví dụ minh họa tính độ dài đoạn AG và GM trong tam giác
AG = (2/3) AM
AG = (2/3) × 12cm = 8cm
Và GM = (1/3) AM hoặc GM = AM – AG
GM = (1/3) × 12cm = 4cm (hoặc GM = 12cm – 8cm = 4cm)
Kết quả: AG = 8cm và GM = 4cm. Đôi khi, việc tập trung vào những điều căn bản giúp giải quyết các vấn đề phức tạp, giống như cách bạn tìm kiếm cua hoàng đế hà nội khi thèm hải sản cao cấp, hay chọn một bài phát biểu nghỉ hưu hay nhất để kết thúc một sự nghiệp thành công.
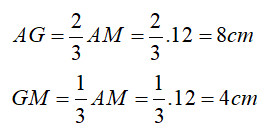Công thức tính toán độ dài AG và GM từ đường trung tuyến AM
Kết Luận
Nắm vững định nghĩa và tính chất của trọng tâm tam giác là nền tảng quan trọng trong việc giải quyết các bài toán hình học. Trọng tâm không chỉ là giao điểm của các đường trung tuyến mà còn có vai trò đặc biệt trong việc phân chia độ dài các đường trung tuyến theo một tỷ lệ cố định. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về trọng tâm của tam giác là gì và cách áp dụng kiến thức này trong thực tế.