Trong hình học, đường chéo là một khái niệm cơ bản nhưng vô cùng quan trọng, không chỉ trong các bài toán lý thuyết mà còn được ứng dụng rộng rãi trong thiết kế, xây dựng, kiến trúc và nhiều lĩnh vực thực tế khác. Đặc biệt, việc hiểu rõ về đường Chéo Hình Chữ Nhật và cách tính của nó là nền tảng giúp chúng ta giải quyết nhiều vấn đề phức tạp.
Bài viết này từ CÔNG TY TNHH MÔI TRƯỜNG HSE sẽ tổng hợp và cung cấp cho bạn những kiến thức chuyên sâu về định nghĩa, tính chất, công thức và ví dụ minh họa về cách tính đường chéo của hình chữ nhật, cũng như hình vuông. Hãy cùng khám phá để áp dụng hiệu quả trong học tập, công việc và cuộc sống!
Đường Chéo Hình Chữ Nhật và Hình Vuông: Khái Niệm Cơ Bản
Đường chéo của hình vuông hoặc hình chữ nhật là đoạn thẳng nối hai đỉnh đối diện của hình đó. Mỗi hình vuông và hình chữ nhật đều có hai đường chéo với độ dài bằng nhau. Chúng đóng vai trò quan trọng trong việc xác định kích thước và đặc điểm hình học của các hình này.
Công Thức Tính Đường Chéo Hình Chữ Nhật Chuẩn Xác
Hình chữ nhật là một tứ giác lồi đặc biệt với bốn góc vuông. Nó cũng là một dạng hình bình hành có hai đường chéo bằng nhau, mang lại nhiều tính chất thú vị và ứng dụng thực tiễn.
Tính chất đường chéo hình chữ nhật
Đường chéo của hình chữ nhật có những tính chất đặc trưng, cực kỳ hữu ích khi giải các bài toán liên quan:
- Độ dài: Độ dài đường chéo của hình chữ nhật chính là cạnh huyền của một tam giác vuông được tạo bởi hai cạnh kề của hình chữ nhật. Do đó, nó bằng căn bậc hai của tổng bình phương hai cạnh (chiều dài và chiều rộng).
- Chia hình: Mỗi đường chéo chia hình chữ nhật thành hai tam giác vuông có diện tích bằng nhau. Điều này cũng có nghĩa là đường chéo không phải là trục đối xứng của hình chữ nhật, tuy nhiên, nó tạo ra sự cân bằng về diện tích.
- Giao điểm: Hai đường chéo của hình chữ nhật có độ dài bằng nhau và cắt nhau tại trung điểm của mỗi đường. Giao điểm này tạo thành bốn tam giác cân, có ý nghĩa quan trọng trong nhiều bài toán chứng minh và tính toán.
Công thức tính đường chéo hình chữ nhật
Để tính độ dài đường chéo hình chữ nhật, chúng ta áp dụng định lý Pytago, một trong những định lý nền tảng nhất của hình học Euclid.
Giả sử bạn có một hình chữ nhật ABCD với chiều dài là a và chiều rộng là b. Đường chéo AC (hoặc BD) sẽ chia hình chữ nhật thành hai tam giác vuông. Chẳng hạn, tam giác ABC là tam giác vuông tại B.
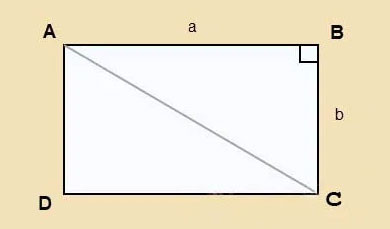Hình chữ nhật với đường chéo AC
Áp dụng định lý Pytago cho tam giác vuông ABC, ta có:
AC² = AB² + BC²
AC² = a² + b²
Từ đó, công thức tính độ dài đường chéo hình chữ nhật có chiều dài a và chiều rộng b là:
Đường chéo = √(a² + b²)
Công thức này cho thấy độ dài đường chéo hình chữ nhật bằng căn bậc hai của tổng bình phương chiều dài và chiều rộng của nó. Đây là một trong những quy tắc hình học cơ bản mà ai cũng cần nắm vững.
Ví dụ minh họa cách tính đường chéo hình chữ nhật
Ví dụ: Tính độ dài đường chéo hình chữ nhật biết chiều dài bằng 10dm và chiều rộng bằng 5dm.
Lời giải:
Gọi độ dài đường chéo hình chữ nhật là d (d > 0, dm).
Áp dụng công thức định lý Pytago, độ dài đường chéo của hình chữ nhật là:
d² = 10² + 5²
d² = 100 + 25
d² = 125
d = √125 = 5√5 dm
Vậy, đường chéo của hình chữ nhật đó dài 5√5 dm.
Đường Chéo Hình Vuông: Kiến Thức Nền Tảng
Hình vuông là trường hợp đặc biệt của hình chữ nhật, khi tất cả bốn cạnh có độ dài bằng nhau. Do đó, các tính chất và cách tính đường chéo của hình vuông cũng có những điểm tương đồng và riêng biệt.
Tính chất đường chéo hình vuông
Đường chéo hình vuông thừa hưởng tất cả tính chất của hình chữ nhật và hình thoi, cùng với những đặc điểm riêng:
- Bằng nhau và vuông góc: Hai đường chéo của hình vuông có độ dài bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Tâm đường tròn: Có một đường tròn nội tiếp và một đường tròn ngoại tiếp hình vuông, đồng thời tâm của cả hai đường tròn này trùng với giao điểm của hai đường chéo.
- Chia tam giác vuông cân: Một đường chéo sẽ chia hình vuông thành hai tam giác vuông cân có diện tích bằng nhau.
- Đường phân giác, trung tuyến, trung trực: Giao điểm của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm duy nhất.
Công thức tính đường chéo hình vuông
Tương tự như hình chữ nhật, chúng ta cũng áp dụng định lý Pytago để tính đường chéo hình vuông.
Giả sử bạn có hình vuông ABCD với độ dài cạnh là a. Đường chéo AC (hoặc BD) sẽ chia hình vuông thành hai tam giác vuông cân, ví dụ tam giác ABC vuông cân tại B.
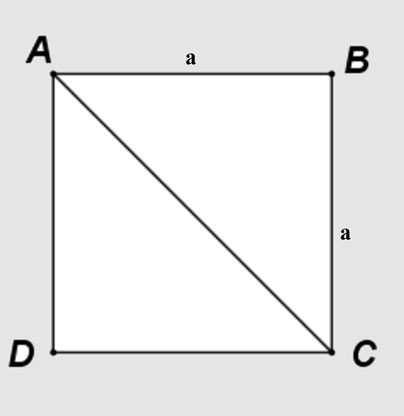Hình vuông với đường chéo AC
Áp dụng định lý Pytago cho tam giác vuông cân ABC:
AC² = AB² + BC²
Vì AB = BC = a (cạnh hình vuông), ta có:
AC² = a² + a² = 2a²
Vậy, công thức tính đường chéo hình vuông có độ dài cạnh a là:
Đường chéo = a√2
Bạn cũng có thể tìm hiểu thêm về công thức tính diện tích hình vuông để có cái nhìn toàn diện hơn về hình học này.
Ví dụ về tính đường chéo hình vuông
Ví dụ 1: Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng bao nhiêu?
Lời giải:
Áp dụng công thức đường chéo hình vuông d = a√2, với a = 3cm.
d = 3√2 cm.
Hoặc áp dụng định lý Pytago:
AC² = 3² + 3² = 9 + 9 = 18
AC = √18 = 3√2 cm.
Ví dụ 2: Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng bao nhiêu?
Lời giải:
Áp dụng công thức d = a√2, ta có:
2 = a√2
a = 2/√2 = √2 dm.
Ứng Dụng Đường Chéo Hình Chữ Nhật Trong Các Bài Toán Thực Tế
Việc hiểu biết về đường chéo hình chữ nhật không chỉ dừng lại ở việc tính toán độ dài mà còn là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong hình học, chẳng hạn như chứng minh một tứ giác là hình chữ nhật. Đây là một mẫu thiết kế đơn giản cho tư duy logic trong toán học.
Ví dụ chứng minh tứ giác là hình chữ nhật:
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, AD. Hỏi tứ giác EFGH là hình gì? Vì sao?
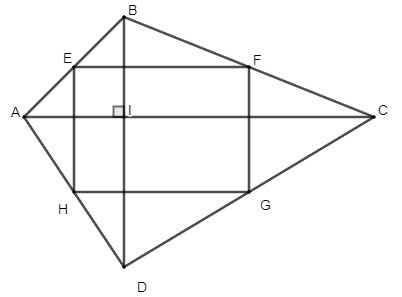Hình ảnh tứ giác ABCD với các trung điểm E, F, G, H tạo thành tứ giác EFGH
Lời giải:
-
Bước 1: Chứng minh EFGH là hình bình hành.
- Vì E là trung điểm của AB, H là trung điểm của AD, nên EH là đường trung bình của tam giác ABD. Từ đó suy ra EH // BD và EH = ½ BD (1).
- Tương tự, F là trung điểm của BC, G là trung điểm của CD, nên FG là đường trung bình của tam giác BCD. Suy ra FG // BD và FG = ½ BD (2).
- Từ (1) và (2), ta có EH // FG và EH = FG.
- Một tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành. Vậy, EFGH là hình bình hành.
-
Bước 2: Chứng minh EFGH có một góc vuông.
- E là trung điểm của AB, F là trung điểm của BC, nên EF là đường trung bình của tam giác ABC. Từ đó suy ra EF // AC.
- Ta đã biết EH // BD (theo Bước 1).
- Theo giả thiết, hai đường chéo của tứ giác ABCD vuông góc với nhau (AC ⊥ BD).
- Vì EH // BD và EF // AC, và AC ⊥ BD, suy ra EH ⊥ EF.
- Một hình bình hành có một góc vuông là hình chữ nhật.
Kết luận: Tứ giác EFGH là hình chữ nhật.
Qua ví dụ này, bạn có thể thấy tầm quan trọng của việc nắm vững các tính chất và công thức hình học trong việc giải quyết các bài toán phức tạp hơn. Việc vận dụng linh hoạt các kiến thức này là một kỹ thuật sắp xếp logic, giúp bạn đạt được kết quả chính xác.
Kết luận
Việc nắm vững kiến thức về đường chéo hình chữ nhật và hình vuông không chỉ là yêu cầu cơ bản trong chương trình học mà còn là nền tảng thiết yếu cho nhiều ứng dụng trong kỹ thuật, xây dựng và thiết kế. Hy vọng qua bài viết này, bạn đã có cái nhìn tổng quan và chi tiết về định nghĩa, tính chất, công thức tính cùng các ví dụ minh họa rõ ràng.
Nếu bạn có nhu cầu tìm hiểu sâu hơn về các công thức hình học khác, hãy tham khảo thêm công thức tính bán kính hình tròn hoặc các bài viết chuyên sâu khác của chúng tôi để mở rộng kiến thức toán học của mình.
Nguồn tham khảo
- Thông tin được tổng hợp và tham khảo từ các kiến thức hình học phổ thông và Quantrimang.com.