Đường cao trong tam giác là một khái niệm hình học nền tảng, đóng vai trò quan trọng trong việc giải quyết nhiều bài toán phức tạp. Đặc biệt, đối với tam giác vuông – một trong những hình tam giác cơ bản nhất, việc hiểu rõ và vận dụng các công thức liên quan đến đường Cao Trong Tam Giác Vuông là cực kỳ cần thiết. Bài viết này của CÔNG TY TNHH MÔI TRƯỜNG HSE sẽ đi sâu vào định nghĩa, các hệ thức lượng quan trọng cùng những ví dụ minh họa chi tiết, giúp bạn nắm vững kiến thức này và áp dụng hiệu quả vào thực tiễn.
Định Nghĩa và Vai Trò Của Đường Cao Trong Tam Giác Vuông
Trong hình học, đường cao của một tam giác là đoạn thẳng hạ từ một đỉnh, vuông góc với cạnh đối diện (gọi là cạnh đáy). Đối với một tam giác vuông, đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền có những tính chất và vai trò đặc biệt, làm phát sinh các hệ thức lượng quan trọng.
Cụ thể, xét tam giác ABC vuông tại A, đường cao AH được kẻ từ đỉnh A xuống cạnh huyền BC. Đoạn AH này không chỉ giúp tính toán diện tích tam giác mà còn là cầu nối giữa các cạnh góc vuông và các hình chiếu của chúng trên cạnh huyền, tạo nên những mối quan hệ toán học chặt chẽ, được gọi là hệ thức lượng trong tam giác vuông.
Các Hệ Thức Lượng Quan Trọng Liên Quan Đến Đường Cao Trong Tam Giác Vuông
Khi nghiên cứu về đường cao trong tam giác vuông, chúng ta không thể bỏ qua các hệ thức lượng sau đây. Đây là những công cụ mạnh mẽ để giải quyết các bài toán liên quan đến độ dài cạnh và đường cao.
Giả sử có tam giác vuông ABC vuông tại A, đường cao AH (với H thuộc BC). Ta có các ký hiệu sau:
- a là độ dài cạnh huyền BC.
- b là độ dài cạnh góc vuông AC.
- c là độ dài cạnh góc vuông AB.
- h là độ dài đường cao AH.
- b’ là độ dài hình chiếu của AC trên BC, tức là đoạn HC.
- c’ là độ dài hình chiếu của AB trên BC, tức là đoạn HB.
Dưới đây là các công thức cơ bản và quan trọng nhất:
-
Định lý Pytago: $a^2 = b^2 + c^2$
Đây là định lý nền tảng, liên hệ ba cạnh của tam giác vuông. -
Hệ thức về cạnh góc vuông và hình chiếu:
- $b^2 = a cdot b’$ (AC² = BC ⋅ HC)
- $c^2 = a cdot c’$ (AB² = BC ⋅ HB)
Công thức này cho biết bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
-
Hệ thức về tích cạnh góc vuông và đường cao:
$a cdot h = b cdot c$ (BC ⋅ AH = AB ⋅ AC)
Tích của cạnh huyền và đường cao tương ứng bằng tích của hai cạnh góc vuông. Đây cũng là một cách để tính diện tích tam giác vuông theo hai phương pháp khác nhau. -
Hệ thức về bình phương đường cao:
$h^2 = b’ cdot c’$ (AH² = HB ⋅ HC)
Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền. -
Hệ thức nghịch đảo bình phương đường cao:
$frac{1}{h^2} = frac{1}{b^2} + frac{1}{c^2}$ (1/AH² = 1/AB² + 1/AC²)
Tổng các nghịch đảo bình phương của hai cạnh góc vuông bằng nghịch đảo bình phương đường cao tương ứng với cạnh huyền.
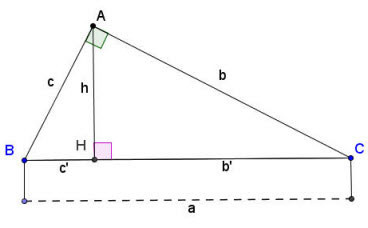Hình ảnh tam giác vuông ABC với đường cao AH
Ví Dụ Minh Họa Cách Tính Đường Cao Trong Tam Giác Vuông
Để hiểu rõ hơn về cách áp dụng các công thức trên, hãy cùng xem qua các ví dụ cụ thể.
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
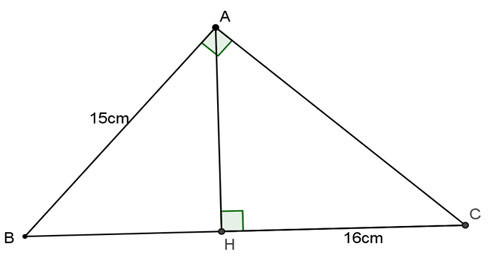Minh họa tam giác vuông ABC và đường cao AH cho ví dụ tính toán
Giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
AC² = CH ⋅ BC = 16 ⋅ BC
Theo định lý Pythagore cho tam giác ABC vuông tại A:
AB² + AC² = BC²
↔ 15² + 16 ⋅ BC = BC²
↔ 225 + 16 ⋅ BC = BC²
↔ BC² – 16 ⋅ BC – 225 = 0
Phương trình bậc hai này có thể giải bằng cách phân tích thành nhân tử:
↔ BC² – 25 ⋅ BC + 9 ⋅ BC – 225 = 0
↔ BC(BC – 25) + 9(BC – 25) = 0
↔ (BC – 25)(BC + 9) = 0
Vì độ dài không thể âm, ta có BC = 25 (cm). (BC = -9 bị loại).
Từ đó: AC² = 16 ⋅ BC = 16 ⋅ 25 = 400 ⇒ AC = 20 (cm).
Để tính đường cao AH, ta sử dụng hệ thức lượng: AH ⋅ BC = AB ⋅ AC
⇒ AH = (AB ⋅ AC) / BC = (15 ⋅ 20) / 25 = 12 (cm).
Vậy, BC = 25cm; AC = 20cm; AH = 12cm.
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 24cm, AC = 32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.
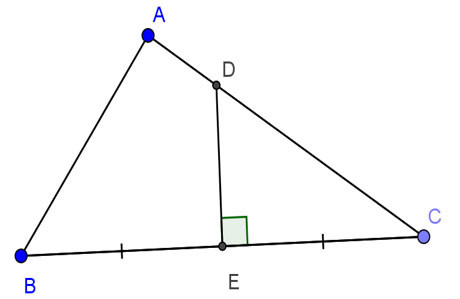Sơ đồ tam giác vuông ABC và đường trung trực DE trong ví dụ 2
Giải:
Xét tam giác vuông ABC, theo định lý Pytago:
BC² = AB² + AC² = 24² + 32² = 576 + 1024 = 1600
⇒ BC = 40 (cm).
Vì DE là đường trung trực của BC nên E là trung điểm của BC, do đó:
EC = BC / 2 = 40 / 2 = 20 (cm).
Xét tam giác vuông ACB và tam giác vuông ECD có:
Góc A = Góc E = 90°
Góc C chung
⇒ Tam giác ACB đồng dạng với tam giác ECD (g.g)
Từ tính chất đồng dạng, ta có tỉ số các cạnh tương ứng:
AC / EC = AB / ED
⇒ ED = (AB ⋅ EC) / AC = (24 ⋅ 20) / 32 = 480 / 32 = 15 (cm).
Vậy DE = 15cm.
Đường Cao Trong Các Loại Tam Giác Khác: Tổng Quan
Mặc dù trọng tâm của chúng ta là đường cao trong tam giác vuông, nhưng việc nắm được cách tính đường cao trong các loại tam giác khác cũng giúp củng cố kiến thức hình học tổng quát.
Đường Cao Trong Tam Giác Thường
Đối với tam giác thường ABC có độ dài ba cạnh a, b, c và nửa chu vi p = (a + b + c) / 2, ta có thể sử dụng công thức Heron để tính diện tích S, sau đó tìm đường cao.
Diện tích S = $sqrt{p(p-a)(p-b)(p-c)}$
Đường cao ứng với cạnh a là $h_a = frac{2S}{a} = 2 frac{sqrt{p(p-a)(p-b)(p-c)}}{a}$
Đường Cao Trong Tam Giác Đều
Tam giác đều có ba cạnh bằng nhau (ký hiệu là a) và ba góc bằng 60 độ. Đường cao trong tam giác đều đồng thời là đường trung tuyến, đường phân giác và đường trung trực.
Công thức tính đường cao h của tam giác đều cạnh a:
$h = a frac{sqrt{3}}{2}$
Đường Cao Trong Tam Giác Cân
Đối với tam giác cân ABC cân tại A, đường cao AH kẻ từ đỉnh A xuống cạnh đáy BC cũng đồng thời là đường trung tuyến, đường phân giác và đường trung trực.
Công thức tính đường cao AH:
Vì tam giác ABC cân tại A nên AH là đường trung tuyến ⇒ HB = HC = ½ BC.
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H:
$AH^2 = AB^2 – BH^2$
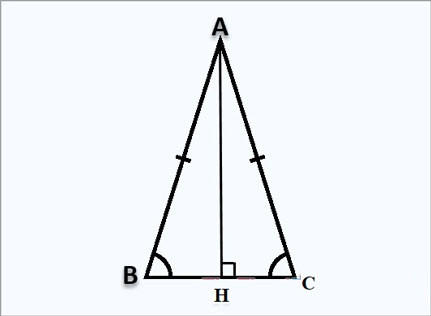Mô tả tam giác cân ABC với đường cao AH
Ví dụ: Cho Δ ABC cân tại A có BC = 30(cm), đường cao AH = 20(cm). Tính độ dài cạnh bên và đường cao ứng với cạnh bên của tam giác cân đó.
Giải: Xét Δ ABC cân tại A có BC = 30(cm) ⇒ BH = CH = 15(cm).
Áp dụng định lý Pytago trong Δ ABH vuông tại H:
$AB = sqrt{(AH^2 + BH^2)} = sqrt{(20^2 + 15^2)} = sqrt{(400 + 225)} = sqrt{625} = 25 (cm)$.
(Đây là công thức tính cạnh AB, từ bài gốc, được dịch sang tiếng Việt và dùng tex.vdoc.vn image cho bước tính toán)
Kẻ đường cao BK vuông góc với AC. Để tính BK, ta sử dụng công thức diện tích.
Diện tích $S{ABC} = frac{1}{2} cdot AH cdot BC = frac{1}{2} cdot 20 cdot 30 = 300 (cm^2)$.
Mặt khác, $S{ABC} = frac{1}{2} cdot BK cdot AC = frac{1}{2} cdot BK cdot 25$.
Do đó, ta có $frac{1}{2} cdot BK cdot 25 = 300$
$BK = frac{2 cdot 300}{25} = frac{600}{25} = 24 (cm)$.
(Đây là công thức tính BK, từ bài gốc, được dịch sang tiếng Việt và dùng tex.vdoc.vn image cho bước tính toán)
Định Nghĩa Chung và Tính Chất Của Đường Cao
Đường cao trong tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao đó. Độ dài của đường cao chính là khoảng cách từ đỉnh đến đáy. Đây là một khái niệm cơ bản nhưng rất quan trọng, không chỉ trong toán học mà còn trong nhiều lĩnh vực kỹ thuật, kiến trúc.
Ba đường cao của bất kỳ tam giác nào cũng luôn cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác. Vị trí của trực tâm sẽ thay đổi tùy thuộc vào loại tam giác:
- Trong tam giác nhọn, trực tâm nằm bên trong tam giác.
- Trong tam giác vuông, trực tâm trùng với đỉnh góc vuông.
- Trong tam giác tù, trực tâm nằm bên ngoài tam giác.
Việc nắm vững các khái niệm và công thức về đường cao, đặc biệt là đường cao trong tam giác vuông, sẽ giúp bạn tự tin giải quyết các bài toán hình học và phát triển tư duy logic. Đừng quên khám phá thêm về [công thức tính diện tích hình vuông](http://moitruonghse.com/cong-thuc-tinh-dien-tich-hin h-vuong/) để mở rộng kiến thức hình học của bạn! Cuộc sống luôn có nhiều điều thú vị để học hỏi, từ những công thức toán học khô khan đến cả những chủ đề thư giãn như truyện tranh nữ giả nam. Dù ở lĩnh vực nào, việc tìm hiểu sâu sắc sẽ mang lại giá trị to lớn.
Kết Luận
Qua bài viết này, CÔNG TY TNHH MÔI TRƯỜNG HSE hy vọng bạn đã có cái nhìn tổng quan và chi tiết về đường cao trong tam giác vuông, từ định nghĩa, các hệ thức lượng cơ bản cho đến các ví dụ minh họa cụ thể. Việc thành thạo các công thức này không chỉ giúp bạn giải quyết tốt các bài tập hình học mà còn là nền tảng vững chắc cho việc tiếp cận những kiến thức toán học phức tạp hơn. Hãy tiếp tục luyện tập và khám phá để trở thành một chuyên gia trong lĩnh vực hình học!
Bạn có thể tìm hiểu thêm các thông tin chuyên sâu khác tại đường cao tam giác vuông và nhiều chủ đề đa dạng khác trên blog của chúng tôi. Chúng tôi luôn nỗ lực mang đến những nội dung chất lượng và hữu ích nhất cho cộng đồng.