Công Thức Tính Diện Tích Hình Vuông Đầy Đủ & Dễ Hiểu Nhất

Hình vuông là một trong những hình học cơ bản và quen thuộc mà chúng ta tiếp xúc từ rất sớm trong chương trình Toán học. Việc nắm vững các đặc điểm, tính chất và đặc biệt là Công Thức Tính Diện Tích Hình Vuông không chỉ giúp bạn giải quyết các bài toán một cách nhanh chóng mà còn đặt nền móng vững chắc cho việc học hình học sau này. Diện tích hình vuông có cách tính siêu đơn giản và dễ nhớ, đây là kiến thức nền tảng quan trọng không thể bỏ qua. Hãy cùng CÔNG TY TNHH MÔI TRƯỜNG HSE khám phá chi tiết về các công thức và ứng dụng của chúng trong bài viết chuyên sâu này, từ đó xây dựng sự tự tin và nâng cao kiến thức toán học của bạn.

Tổng Quan Về Hình Vuông: Định Nghĩa Và Tính Chất Cần Nhớ

Trước khi đi sâu vào các công thức tính diện tích, việc hiểu rõ bản chất và ghi nhớ các tính chất của hình vuông là vô cùng quan trọng. Đây là nền tảng để bạn có thể áp dụng công thức một cách chính xác và linh hoạt trong nhiều dạng bài tập khác nhau. Hãy cùng chúng tôi tìm hiểu những thông tin cơ bản về hình vuông dưới đây.

Hình Vuông Là Gì?

Hình vuông là một dạng hình học phẳng đặc biệt, thuộc nhóm tứ giác, và nó được định nghĩa bởi các đặc điểm cốt lõi sau:

Các cạnh có cùng độ dài: Tất cả bốn cạnh của hình vuông đều bằng nhau. Đây là đặc điểm nổi bật giúp phân biệt nó với các hình tứ giác khác.
Các góc trong đều là góc vuông: Mỗi góc trong của hình vuông đều có độ lớn chính xác là 90 độ. Điều này có nghĩa là các góc đều bằng nhau và vuông góc với nhau.
Đường chéo: Hai đường chéo của hình vuông cắt nhau tại một điểm, chia mỗi góc trong thành hai góc bằng nhau (45 độ). Chúng cũng vuông góc với nhau và có độ dài bằng nhau.

Với những đặc điểm này, hình vuông có thể được xem là một trường hợp đặc biệt của hình chữ nhật (khi tất cả các cạnh bằng nhau) và cũng là một trường thoi (khi tất cả các góc bằng nhau). Tính đồng nhất của các cạnh và góc vuông khiến hình vuông trở thành một hình học cơ bản, được ứng dụng rộng rãi trong nhiều lĩnh vực, từ toán học, kiến trúc, kỹ thuật đến nghệ thuật.

Định nghĩa và các tính chất cơ bản của hình vuông trong hình học

Các Tính Chất Nổi Bật Của Hình Vuông

Hình vuông sở hữu nhiều tính chất đặc biệt giúp chúng ta dễ dàng nhận diện và thực hiện các phép tính liên quan. Dưới đây là một số tính chất quan trọng mà bạn cần ghi nhớ:

Cạnh và góc: Tất cả bốn cạnh của hình vuông có độ dài bằng nhau và tất cả bốn góc trong đều bằng 90 độ (góc vuông).
Đường chéo: Hình vuông có hai đường chéo bằng nhau, cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Mỗi đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau. Độ dài đường chéo (d) được tính bằng công thức: d = a × √2 (trong đó a là độ dài cạnh hình vuông).
Chu vi và diện tích:
- Chu vi (P) của hình vuông được tính bằng công thức: P = 4 × a.
- Diện tích (S) của hình vuông được tính bằng công thức: S = a × a hoặc S = a².
Đối xứng và đường phân giác: Hình vuông có 4 trục đối xứng (hai đường chéo và hai đường nối trung điểm các cạnh đối diện). Nó cũng có tâm đối xứng chính là giao điểm của hai đường chéo. Các đường chéo đồng thời là đường phân giác của các góc của hình vuông.
Đồng dạng: Tất cả các hình vuông đều đồng dạng với nhau, tức là chúng có cùng tỷ lệ về cạnh và góc, chỉ khác nhau về kích thước.
Liên hệ với hình 3D: Nếu hình vuông là mặt đáy hoặc mặt bên của một khối hình hộp, nó sẽ tạo thành khối lập phương (nếu tất cả các mặt là hình vuông) hoặc các khối hình hộp chữ nhật.

Việc ghi nhớ và hiểu rõ những tính chất này sẽ giúp bạn giải quyết các bài toán liên quan đến hình vuông một cách nhanh chóng và chính xác, đồng thời phát triển tư duy logic trong hình học. Để nâng cao hơn nữa kiến thức hình học cho cấp tiểu học, bạn có thể tham khảo thêm bài viết về tính chu vi, diện tích hình vuông lớp 4 để củng cố nền tảng.

Công Thức Tính Diện Tích Hình Vuông Chi Tiết

Với những đặc tính riêng biệt, công thức tính diện tích hình vuông cũng rất đặc biệt và dễ nhớ. Nếu bạn đã quen thuộc với cách tính diện tích hình chữ nhật thì diện tích hình vuông sẽ có nét tương đồng. Sau đây, chúng tôi sẽ hướng dẫn bạn cách tính diện tích hình vuông một cách đơn giản, kèm theo ví dụ minh họa dễ hiểu.

Công Thức Tính Diện Tích Hình Vuông Theo Cạnh (a)

Đây là công thức cơ bản và phổ biến nhất để tính diện tích hình vuông. Khi biết độ dài một cạnh của hình vuông, bạn có thể dễ dàng xác định diện tích của nó.

Công thức:

Công thức tính diện tích hình vuông S bằng cạnh nhân cạnh (a x a)

Diện tích hình vuông = cạnh × cạnh

Trong đó:

S là ký hiệu của diện tích hình vuông.
a là ký hiệu của độ dài một cạnh của hình vuông.

Công thức này có thể được viết gọn lại là:

S = a × a

hoặc

S = a²

Ví dụ:
Nếu hình vuông có cạnh a là 5 cm, ta có thể tính diện tích như sau:
S = 5 × 5
Hoặc S = 5²
Do đó, diện tích của hình vuông có cạnh là 5 cm là 25 cm².

Công Thức Tính Diện Tích Hình Vuông Khi Biết Độ Dài Đường Chéo (d)

Trong một số trường hợp, chúng ta không biết độ dài cạnh của hình vuông mà chỉ biết độ dài đường chéo. Khi đó, bạn vẫn có thể tính toán diện tích hình vuông bằng một công thức khác.

Công thức:

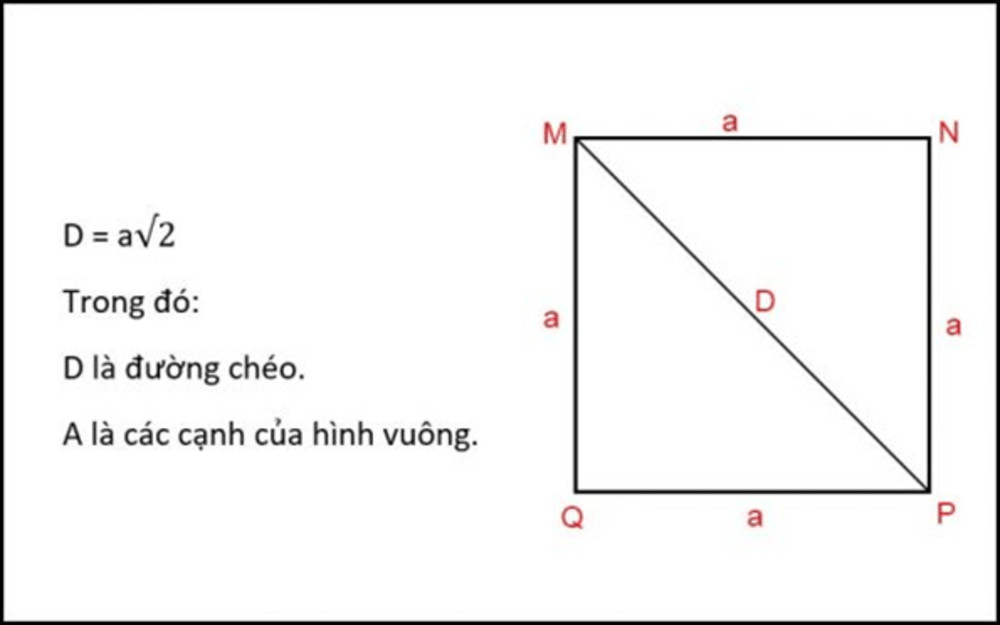Minh họa công thức tính diện tích hình vuông từ độ dài đường chéo d

Diện tích = (d²) / 2

Trong đó:

S là ký hiệu của diện tích hình vuông.
d là ký hiệu của độ dài đường chéo của hình vuông.

Giải thích:
Như đã đề cập trong phần tính chất, đường chéo của hình vuông (d) có mối quan hệ với cạnh (a) theo công thức d = a × √2. Từ đó, ta có thể suy ra a = d / √2.
Khi đó, S = a × a = (d / √2) × (d / √2) = d² / (√2 × √2) = d² / 2.
Đây là một công thức rất hữu ích trong các bài toán nâng cao hơn.

Ví dụ:
Nếu biết đường chéo của hình vuông là 10 cm, ta có thể tính diện tích như sau:
Diện tích = (10²) / 2
Diện tích = 100 / 2
Diện tích = 50 cm²
Do đó, diện tích của hình vuông khi biết đường chéo là 10 cm là 50 cm².

Các Dạng Bài Tập Tính Diện Tích Hình Vuông Thường Gặp

Từ những công thức tính diện tích hình vuông ở trên, bạn sẽ thường xuyên gặp phải một số dạng bài tập cơ bản đến nâng cao. Mặc dù công thức tính S hình vuông đơn giản, nhưng một số dạng bài có thể đòi hỏi tư duy logic và suy luận để tìm ra các yếu tố cần thiết.

Cách Tính Diện Tích Hình Vuông Khi Biết Chu Vi (P)

Khi chu vi của hình vuông được cho trước, bạn hoàn toàn có thể tìm được diện tích của nó thông qua các bước đơn giản.

Các bước thực hiện:

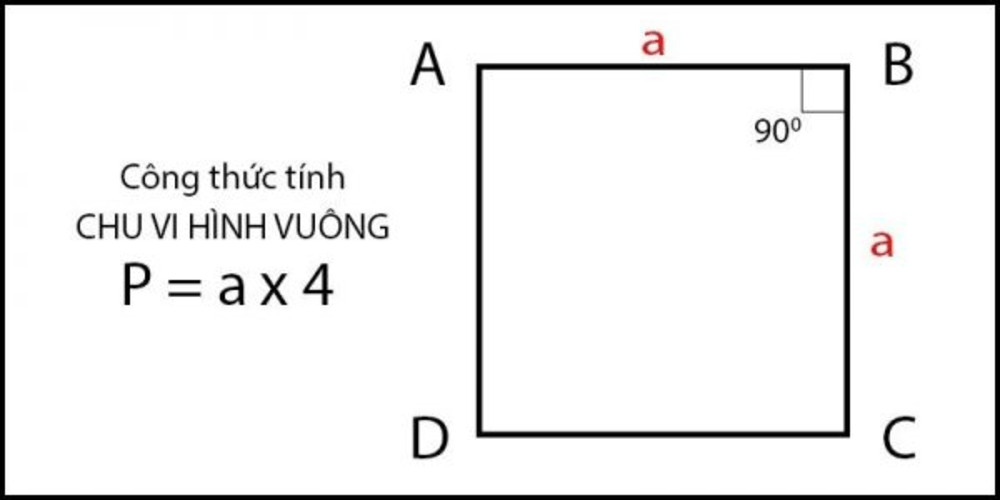Cách tính diện tích hình vuông khi đã biết chu vi P

Tìm độ dài cạnh (a) của hình vuông:
- Chu vi của hình vuông (P) được tính bằng tổng độ dài của bốn cạnh, tức là P = 4 × a.
- Từ đó, độ dài cạnh a sẽ là a = P / 4.
Tính diện tích (S) của hình vuông:
- Sau khi tìm được độ dài cạnh a, bạn áp dụng công thức cơ bản: S = a × a hoặc S = a².

Ví dụ:
Nếu biết chu vi của hình vuông là 20 cm, ta có thể tính diện tích như sau:

Bước 1: Tính độ dài cạnh (a) của hình vuông.
a = P / 4 = 20 / 4
=> a = 5 cm
Bước 2: Tính diện tích (S) của hình vuông.
S = a × a = 5 × 5
=> S = 25 cm²
Để khám phá thêm nhiều dạng kiến thức khác, đôi khi không liên quan đến toán học nhưng vẫn rất thú vị, bạn có thể tham khảo thêm về tử vi tuổi Kỷ Mùi 2024.

Cách Tính Diện Tích Hình Vuông Nội Tiếp Hình Tròn

Trong hình học, một hình vuông nội tiếp hình tròn là hình vuông nằm hoàn toàn bên trong hình tròn và tất cả các đỉnh của hình vuông đều nằm trên đường tròn. Để tính diện tích hình vuông trong trường hợp này, ta cần biết thông tin về hình tròn.

Các bước thực hiện:

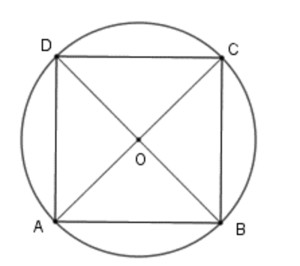Công thức tính diện tích hình vuông nội tiếp trong một hình tròn

Xác định đường kính hoặc bán kính của hình tròn:
- Nếu biết bán kính (r), đường kính (D) là D = 2 × r.
- Nếu biết đường kính (D), bán kính (r) là r = D / 2.
Tìm độ dài cạnh của hình vuông:
- Trong trường hợp hình vuông nội tiếp hình tròn, đường chéo (d) của hình vuông chính bằng đường kính (D) của hình tròn. Tức là d = D.
- Sau đó, từ đường chéo d, ta có thể tìm cạnh a của hình vuông bằng công thức: a = d / √2.
Tính diện tích (S) của hình vuông:
- Áp dụng công thức cơ bản: S = a × a hoặc S = a².
- Ngoài ra, bạn cũng có thể trực tiếp áp dụng công thức S = d² / 2 (với d = D). Tức là S = D² / 2.

Ví dụ:
Nếu biết hình tròn có đường kính D là 10 cm, ta có thể tính diện tích hình vuông nội tiếp hình tròn như sau:

Bước 1: Đường kính của hình tròn D = 10 cm. (Nếu đề bài cho bán kính r, bạn cần tính D = 2r)
Bước 2: Xác định độ dài cạnh (a) hoặc đường chéo (d) của hình vuông.
Vì hình vuông nội tiếp hình tròn, đường chéo của hình vuông chính bằng đường kính của hình tròn.
d = D = 10 cm.
Áp dụng công thức S = d² / 2:
S = (10²) / 2 = 100 / 2 = 50 cm²

Hoặc, nếu muốn tìm cạnh trước:
a = d / √2 = 10 / √2 ≈ 7.07 cm
S = a × a ≈ 7.07 × 7.07 ≈ 50 cm²

Tính Diện Tích Hình Vuông Trong Lập Trình Pascal

Pascal là một ngôn ngữ lập trình phổ biến, thường được dạy trong chương trình tin học ở cấp trung học. Việc tính diện tích hình vuông trong Pascal là một dạng bài tập cơ bản giúp học sinh làm quen với các khái niệm biến, nhập xuất dữ liệu và phép toán.

Cách lập trình để tính diện tích hình vuông trong Pascal:

Mô tả cách lập trình tính diện tích hình vuông bằng ngôn ngữ Pascal

Dưới đây là một ví dụ đơn giản về chương trình Pascal để tính diện tích hình vuông:

program TinhDienTichHinhVuong;

var
  canh, dienTich: real; // Khai báo biến 'canh' và 'dienTich' kiểu số thực

begin
  // Nhập độ dài cạnh của hình vuông từ bàn phím
  writeln('Nhap do dai canh cua hinh vuong: ');
  readln(canh);

  // Tính diện tích của hình vuông
  dienTich := canh * canh;

  // Hiển thị kết quả
  writeln('Dien tich cua hinh vuong la: ', dienTich:0:2); // Định dạng hiển thị 2 chữ số thập phân

  // Tạm dừng chương trình để xem kết quả
  readln;
end.

Giải thích chương trình:

program TinhDienTichHinhVuong;: Dòng này khai báo tên của chương trình.
var canh, dienTich: real;: Khai báo hai biến canh (để lưu độ dài cạnh) và dienTich (để lưu kết quả diện tích). Kiểu real được sử dụng để cho phép nhập và tính toán với số thập phân. Bạn có thể dùng integer nếu chỉ làm việc với số nguyên.
writeln('Nhap do dai canh cua hinh vuong: ');: Hiển thị thông báo yêu cầu người dùng nhập độ dài cạnh.
readln(canh);: Đọc giá trị người dùng nhập từ bàn phím và gán vào biến canh.
dienTich := canh * canh;: Thực hiện phép tính diện tích bằng cách nhân canh với chính nó và gán kết quả cho biến dienTich.
writeln('Dien tich cua hinh vuong la: ', dienTich:0:2);: Hiển thị kết quả diện tích lên màn hình. Phần :0:2 là định dạng để hiển thị số thực với 2 chữ số thập phân.
readln;: Tạm dừng chương trình để người dùng có thể xem kết quả trước khi chương trình tự đóng.

Chương trình này minh họa rõ ràng cách áp dụng công thức S = a × a vào môi trường lập trình, giúp bạn hình dung cách chuyển đổi kiến thức toán học sang mã máy. Tìm hiểu thêm các chủ đề đa dạng khác như bộ tam sên để mở rộng hiểu biết.

Những Lưu Ý Quan Trọng Khi Tính Diện Tích Hình Vuông

Trong quá trình giải bài tập hay thực hiện các phép tính liên quan đến diện tích hình vuông, đôi khi bạn có thể mắc phải những sai sót nhỏ nếu không chú ý đến các yếu tố quan trọng. Dưới đây là một số lưu ý cần thiết để đảm bảo tính chính xác cho kết quả của bạn:

Những lưu ý quan trọng để tính diện tích hình vuông chính xác

Đơn vị đo lường: Luôn đảm bảo rằng bạn đang sử dụng cùng một đơn vị đo lường cho tất cả các đại lượng trong bài toán. Ví dụ, nếu cạnh được đo bằng mét (m), thì diện tích sẽ được tính bằng mét vuông (m²). Nếu cạnh là centimet (cm), diện tích là centimet vuông (cm²). Việc sai lệch đơn vị có thể dẫn đến kết quả sai hoàn toàn.
Tính toán chính xác: Khi sử dụng máy tính bỏ túi hoặc mã lập trình, hãy chắc chắn rằng bạn đã nhập đúng các giá trị và thực hiện đúng phép toán (nhân cạnh với chính nó hoặc bình phương cạnh). Đối với lập trình, hãy kiểm tra kiểu dữ liệu (số nguyên hoặc số thực) để tránh lỗi tràn số hoặc mất độ chính xác.
Định dạng kết quả: Khi trình bày kết quả, hãy luôn ghi rõ đơn vị đo lường của diện tích (ví dụ: cm², m², km²). Điều này không chỉ giúp kết quả rõ ràng mà còn thể hiện sự cẩn thận và hiểu biết của bạn.
Trong hình tròn: Khi tính diện tích hình vuông nội tiếp hình tròn, hãy xác định chính xác đường kính hoặc bán kính của hình tròn trước. Sai lầm trong bước này sẽ kéo theo sai lầm trong việc xác định cạnh hoặc đường chéo của hình vuông và cuối cùng là sai diện tích.
Kiểm tra lại kết quả: Nếu có thời gian, hãy thử kiểm tra lại kết quả bằng cách sử dụng phương pháp khác (ví dụ: nếu bạn tính diện tích từ cạnh, thử tính ngược lại để xem cạnh có đúng không, hoặc nếu có thể, dùng công thức từ đường chéo). Việc này giúp tăng cường độ tin cậy của kết quả.
Tìm hiểu thêm: Để mở rộng kiến thức và có cái nhìn tổng quan hơn về các chủ đề khác trong cuộc sống, bạn có thể tham khảo thêm thông tin về khu công nghiệp Tam Phước để biết thêm về các dự án phát triển kinh tế và công nghiệp. Ngoài ra, thế giới giải trí cũng đa dạng không kém, ví dụ như những tác phẩm truyện tranh nữ giả nam thu hút một lượng lớn độc giả.

Những lưu ý trên sẽ giúp bạn thực hiện các phép tính diện tích hình vuông một cách chính xác, tự tin hơn và tránh được những sai sót không đáng có.

Bài Tập Mẫu Về Diện Tích Hình Vuông Kèm Lời Giải Chi Tiết

Để củng cố kiến thức và rèn luyện kỹ năng áp dụng các công thức tính diện tích hình vuông, hãy cùng chúng tôi thực hành qua một số bài tập mẫu điển hình dưới đây. Bạn có thể tự giải trước khi so sánh với lời giải chi tiết để kiểm tra sự hiểu biết của mình.

Bài Tập 1: Diện Tích Hình Vuông Cơ Bản (Lớp 3)

Bài tập: Tính diện tích của một hình vuông có cạnh là 6 dm.

Lời giải:

Để tính diện tích của hình vuông, ta sử dụng công thức cơ bản: Diện tích = cạnh × cạnh.

Độ dài cạnh của hình vuông (a) = 6 dm.
Áp dụng công thức:
Diện tích = a × a
=> Diện tích = 6 × 6
Diện tích = 36 dm²

Vậy, diện tích của hình vuông là 36 dm².

Bài Tập 2: Tính Diện Tích Hình Vuông Từ Đường Chéo

Bài tập: Tính diện tích của một hình vuông khi biết độ dài đường chéo là 10 cm.

Lời giải:

Để tính diện tích của hình vuông khi biết đường chéo, ta có thể sử dụng công thức trực tiếp S = d² / 2.

Độ dài đường chéo của hình vuông (d) = 10 cm.
Áp dụng công thức:
Diện tích = (d²) / 2
=> Diện tích = (10²) / 2
=> Diện tích = 100 / 2
Diện tích = 50 cm²

Vậy, diện tích của hình vuông là 50 cm².

(Lưu ý: Nếu bạn muốn giải bằng cách tìm cạnh trước, thì cạnh a = d/√2 = 10/√2 ≈ 7.07 cm. Khi đó, S = a × a ≈ 7.07 × 7.07 ≈ 50 cm². Kết quả là như nhau.)

Bài Tập 3: Diện Tích Hình Vuông Trong Hệ Tọa Độ Oxy

Bài tập: Cho hình vuông có các đỉnh là A(2, 3), B(5, 3), C(5, 6), và D(2, 6). Hãy tính diện tích của hình vuông trong hệ tọa độ Oxy.

Lời giải:

Để tính diện tích của hình vuông trong hệ tọa độ Oxy, ta cần tìm độ dài cạnh của hình vuông dựa vào tọa độ các đỉnh, sau đó sử dụng công thức diện tích hình vuông.

Bước 1: Tìm độ dài cạnh (a) của hình vuông ABCD.
Ta có thể tính khoảng cách giữa hai điểm trong mặt phẳng Oxy. Chọn cạnh AB hoặc BC.
Sử dụng công thức khoảng cách giữa hai điểm (x1, y1) và (x2, y2):
Khoảng cách = √[(x2 – x1)² + (y2 – y1)²]
Tính độ dài cạnh AB với A(2, 3) và B(5, 3):
a = √[(5 – 2)² + (3 – 3)²] => a = √[3² + 0²] => a = √9
=> a = 3 đơn vị
Bước 2: Áp dụng công thức để tính diện tích.
Diện tích = a × a
=> Diện tích = 3 × 3
Diện tích = 9 đơn vị vuông

Vậy, diện tích của hình vuông trong hệ tọa độ Oxy là 9 đơn vị vuông.

Bài Tập 4: Diện Tích Hình Vuông Nội Tiếp Hình Tròn

Bài tập: Cho một hình tròn có bán kính là 5 cm. Hãng tính diện tích của hình vuông nằm trong hình tròn (nội tiếp).

Lời giải:

Khi hình vuông nội tiếp hình tròn, đường chéo của hình vuông chính là đường kính của hình tròn. Từ đó, ta có thể tính diện tích hình vuông.

Bán kính của hình tròn (r) = 5 cm.
Bước 1: Xác định đường kính (D) của hình tròn.
D = 2 × r = 2 × 5 = 10 cm.
Bước 2: Xác định độ dài đường chéo (d) của hình vuông.
Vì hình vuông nội tiếp hình tròn, d = D = 10 cm.
Bước 3: Áp dụng công thức tính diện tích hình vuông từ đường chéo.
Diện tích = (d²) / 2
=> Diện tích = (10²) / 2
=> Diện tích = 100 / 2
Diện tích = 50 cm²

Vậy, diện tích của hình vuông nội tiếp hình tròn là 50 cm².

Kết Luận

Việc nắm vững công thức tính diện tích hình vuông và các dạng bài tập liên quan là nền tảng quan trọng trong hành trình học toán. Với những kiến thức từ định nghĩa, tính chất, các công thức cơ bản đến nâng cao (như tính từ đường chéo, chu vi, hoặc trong hệ tọa độ/lập trình) mà chúng tôi đã chia sẻ, hy vọng bạn đã có cái nhìn tổng quan và chi tiết nhất.

Để thực sự thành thạo, hãy chăm chỉ luyện tập các bài tập, đặc biệt là các dạng bài tập mẫu có lời giải chi tiết. Luôn nhớ kiểm tra đơn vị và kết quả để đảm bảo độ chính xác. CÔNG TY TNHH MÔI TRƯỜNG HSE mong rằng bài viết này sẽ là tài liệu hữu ích, giúp bạn có những giờ học vui vẻ và hiệu quả, đồng thời tự tin chinh phục các thử thách trong môn Toán. Chúc bạn luôn thành công trên con đường tìm kiếm tri thức!

Nguồn tham khảo: Bài viết từ The Dewey Schools.

Blogs

Công Thức Tính Diện Tích Hình Vuông Đầy Đủ & Dễ Hiểu Nhất

Tổng Quan Về Hình Vuông: Định Nghĩa Và Tính Chất Cần Nhớ

Hình Vuông Là Gì?

Các Tính Chất Nổi Bật Của Hình Vuông

Công Thức Tính Diện Tích Hình Vuông Chi Tiết

Công Thức Tính Diện Tích Hình Vuông Theo Cạnh (a)

Công Thức Tính Diện Tích Hình Vuông Khi Biết Độ Dài Đường Chéo (d)

Các Dạng Bài Tập Tính Diện Tích Hình Vuông Thường Gặp

Cách Tính Diện Tích Hình Vuông Khi Biết Chu Vi (P)

Cách Tính Diện Tích Hình Vuông Nội Tiếp Hình Tròn

Tính Diện Tích Hình Vuông Trong Lập Trình Pascal

Những Lưu Ý Quan Trọng Khi Tính Diện Tích Hình Vuông

Bài Tập Mẫu Về Diện Tích Hình Vuông Kèm Lời Giải Chi Tiết

Bài Tập 1: Diện Tích Hình Vuông Cơ Bản (Lớp 3)

Bài Tập 2: Tính Diện Tích Hình Vuông Từ Đường Chéo

Bài Tập 3: Diện Tích Hình Vuông Trong Hệ Tọa Độ Oxy

Bài Tập 4: Diện Tích Hình Vuông Nội Tiếp Hình Tròn

Kết Luận

Để lại một bình luận Hủy

Đăng nhập