Hệ thức lượng trong tam giác vuông là một trong những kiến thức toán học cơ bản và vô cùng quan trọng đối với học sinh lớp 9. Việc nắm vững các công thức này không chỉ giúp bạn giải quyết nhanh chóng các bài tập mà còn xây dựng nền tảng vững chắc cho các kiến thức hình học phức tạp hơn. Bài viết này của chúng tôi sẽ tổng hợp các hệ thức lượng cần thiết, các định lý quan trọng, và hướng dẫn giải chi tiết các dạng bài tập tiêu biểu, giúp bạn dễ dàng nắm bắt và áp dụng hiệu quả.
1. Các Hệ Thức Liên Quan Đến Cạnh Và Đường Cao Trong Tam Giác Vuông
Trong một tam giác vuông ABC vuông tại A, với AH là đường cao kẻ từ đỉnh A xuống cạnh huyền BC, các bạn học sinh lớp 9 cần ghi nhớ các hệ thức liên quan sau đây:
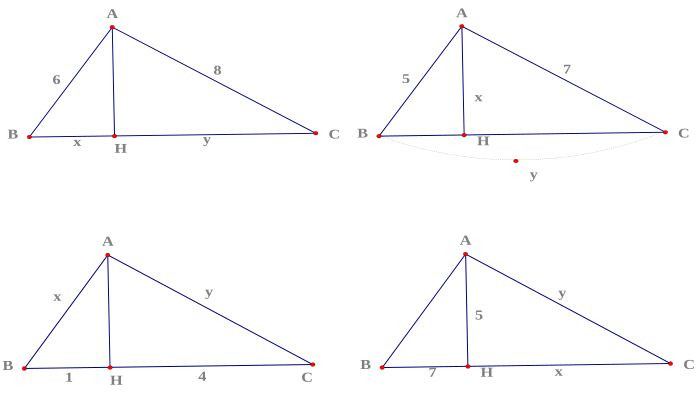Các hệ thức liên quan đến hệ thức lượng trong tam giác vuông
Nếu ký hiệu các cạnh góc vuông là b (AC), c (AB), cạnh huyền là a (BC), đường cao là h (AH), hình chiếu của cạnh góc vuông AB lên cạnh huyền BC là c’ (BH), và hình chiếu của cạnh góc vuông AC lên cạnh huyền BC là b’ (CH), ta có:
- Hệ thức 1: Bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
- $AB^2 = BH cdot BC Rightarrow c^2 = c’ cdot a$
- $AC^2 = CH cdot BC Rightarrow b^2 = b’ cdot a$
- Hệ thức 2: Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
- $AH^2 = BH cdot CH Rightarrow h^2 = c’ cdot b’$
- Hệ thức 3: Tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
- $AB cdot AC = AH cdot BC Rightarrow c cdot b = h cdot a$
- Hệ thức 4 (Nghịch đảo bình phương đường cao): Nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo bình phương của hai cạnh góc vuông.
- $frac{1}{AH^2} = frac{1}{AB^2} + frac{1}{AC^2} Rightarrow frac{1}{h^2} = frac{1}{c^2} + frac{1}{b^2}$
- Định lý Pytago: Bình phương cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
- $BC^2 = AB^2 + AC^2 Rightarrow a^2 = c^2 + b^2$
Để hiểu rõ hơn về cách xác định và vận dụng đường cao trong các dạng toán hình học, bạn có thể tham khảo thêm bài viết về đường cao trong tam giác.
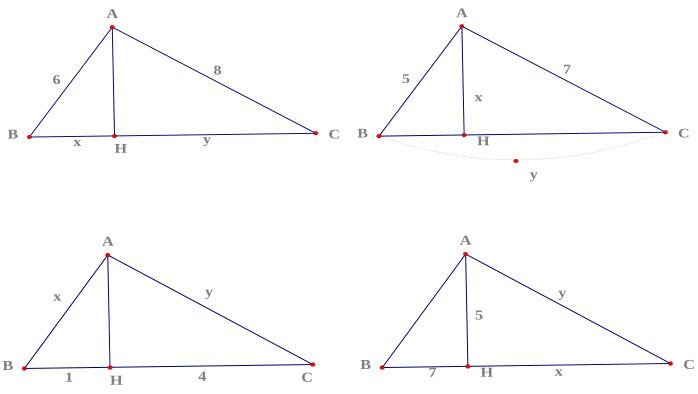Các hệ thức liên quan đến hệ thức lượng trong tam giác vuông và tam giác thường
2. Tỷ Số Lượng Giác Của Góc Nhọn Trong Tam Giác Vuông
Một số kiến thức quan trọng có liên quan đến các công thức lượng giác và hệ thức lượng tam giác vuông mà chúng tôi chuẩn bị nhắc tới như sau:
2.1. Định Nghĩa Về Tỷ Số Lượng Giác
Trong một tam giác vuông, với một góc nhọn $alpha$:
- Sin alpha ($sin alpha$) = Cạnh đối / Cạnh huyền
- Cos alpha ($cos alpha$) = Cạnh kề / Cạnh huyền
- Tan alpha ($tan alpha$) = Cạnh đối / Cạnh kề
- Cot alpha ($cot alpha$) = Cạnh kề / Cạnh đối
2.2. Định Lý Về Tỷ Số Lượng Giác
Trong một tam giác vuông, nếu hai góc nhọn là hai góc phụ nhau (có tổng số đo bằng 90 độ) thì:
- Sin góc này bằng Cos góc kia.
- Tan góc này bằng Cot góc kia.
- Và ngược lại.
Ví dụ: Nếu $alpha + beta = 90^circ$ thì $sin alpha = cos beta$, $tan alpha = cot beta$.
2.3. Các So Sánh Cần Nhớ Của Hệ Số Lượng Giác
Cho hai góc nhọn $alpha$ và $beta$ của một tam giác vuông, tức là $alpha + beta = 90^circ$. Nếu $alpha < beta$ thì:
- $sin alpha < sin beta$
- $cos alpha > cos beta$
- $tan alpha < tan beta$
- $cot alpha > cot beta$
Nắm vững kiến thức để làm bài dễ dàng hơn
3. Các Hệ Thức Cơ Bản Giữa Các Tỷ Số Lượng Giác
Nếu $alpha$ là một góc nhọn bất kỳ, ta có các hệ thức cơ bản sau:
- $0 < sin alpha < 1$
- $0 < cos alpha < 1$
- $tan alpha > 0$
- $cot alpha > 0$
- $sin^2 alpha + cos^2 alpha = 1$
- $tan alpha cdot cot alpha = 1$
- $tan alpha = frac{sin alpha}{cos alpha}$
- $cot alpha = frac{cos alpha}{sin alpha}$
- $1 + tan^2 alpha = frac{1}{cos^2 alpha}$
- $1 + cot^2 alpha = frac{1}{sin^2 alpha}$
4. Hướng Dẫn Một Số Dạng Bài Tập Hệ Thức Lượng Trong Tam Giác
Dưới đây là một số dạng bài tập tiêu biểu đại diện cho việc áp dụng các hệ thức lượng trong tam giác vuông lớp 9 được nêu ra ở trên:
4.1. Chứng Minh Các Hệ Thức Và Tính Giá Trị Của Biểu Thức
Phương pháp giải:
Vận dụng các phương pháp chứng minh đẳng thức như biến đổi một vế bằng vế kia, biến đổi cả hai vế về cùng một biểu thức trung gian, hoặc từ giả thiết ban đầu suy ra đẳng thức cần chứng minh. Áp dụng linh hoạt các định lý trong tam giác vuông, tam giác thường và các hệ thức lượng giác đã học.
4.2. Tính Toán Các Đại Lượng
Phương pháp giải:
Vận dụng các công thức tính sin, cos, tan, cot, các định lý về đường trung tuyến, công thức tính diện tích và các mối liên hệ giữa các đại lượng cần tính. Đặc biệt chú ý đến các tính chất của các tam giác đặc biệt (ví dụ: tam giác vuông cân, tam giác đều).
4.3. Chứng Minh Tam Giác
Phương pháp giải:
Sử dụng các hệ thức lượng giác, các định lý, công thức diện tích, đường trung tuyến, các bất phương trình cơ bản và hằng số để chứng minh các tính chất hoặc loại tam giác theo yêu cầu bài toán.
4.4. Các Bài Toán Thực Tế Về Giải Tam Giác
Phương pháp giải cụ thể:
Giải tam giác là việc tìm số đo các cạnh và góc còn lại trong tam giác khi biết một số giả thiết nhất định. Vận dụng tổng hợp các hệ thức lượng, định lý, công thức diện tích, đường trung tuyến đã học. Đối với bài toán thực tế, cần biểu diễn tình huống thực tế bằng mô hình tam giác và xác định các đại lượng cần tính.
6. Tổng Hợp Bài Tập Vận Dụng Và Hướng Dẫn Giải Chi Tiết
Top những dạng toán hay ra trong đề kiểm tra nhất hiện nay
Bài 1: Cho tam giác vuông ABC vuông tại A, có đường cao AH của tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài lần lượt là 3 và 4. Vận dụng các quan hệ đã học ở phần trên để tính các cạnh góc vuông của tam giác ABC.
Lời giải:
Ở bài toán này, trước tiên ta cần xét các yếu tố dữ kiện mà bài toán đã cho: tam giác ABC vuông tại A, đường cao AH, BH = 3, CH = 4. Từ đó, cạnh huyền BC = BH + CH = 3 + 4 = 7.
Chúng ta sẽ sử dụng hệ thức liên quan giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền:
- $AB^2 = BH cdot BC = 3 cdot 7 = 21 Rightarrow AB = sqrt{21}$
- $AC^2 = CH cdot BC = 4 cdot 7 = 28 Rightarrow AC = sqrt{28} = 2sqrt{7}$
Vậy, độ dài hai cạnh góc vuông là $sqrt{21}$ và $2sqrt{7}$.
Bài tập 2: Cho tam giác ABC vuông tại A có cạnh góc vuông kề với góc $60^circ$ của tam giác vuông này bằng 3. Sử dụng bảng lượng giác các góc đặc biệt để tìm cạnh huyền và cạnh góc vuông còn lại (Lưu ý bạn cần phải làm tròn số vừa tính đến chữ số thập phân thứ tư nhé).
Giải:
Giả sử cạnh góc vuông kề với góc $60^circ$ là cạnh AB. Vậy, góc B = $60^circ$. Vì tam giác ABC vuông tại A, nên góc C = $90^circ – 60^circ = 30^circ$. Cạnh AB = 3.
- Để tìm cạnh huyền BC, ta sử dụng $cos B = frac{AB}{BC}$.
$cos 60^circ = frac{3}{BC} Rightarrow BC = frac{3}{cos 60^circ} = frac{3}{0.5} = 6$. - Để tìm cạnh góc vuông AC, ta sử dụng $tan B = frac{AC}{AB}$.
$tan 60^circ = frac{AC}{3} Rightarrow AC = 3 cdot tan 60^circ = 3 cdot sqrt{3} approx 3 cdot 1.7320508 approx 5.1961524$.
Làm tròn đến chữ số thập phân thứ tư: $AC approx 5.1962$.
Vậy, cạnh huyền BC = 6 và cạnh góc vuông AC $approx 5.1962$.
Bài 3: Vận dụng kiến thức đã học viết các tỷ số lượng giác sau thành các tỷ số lượng giác của các góc nhỏ hơn $45^circ$, gồm $sin 60^circ$, $cos 75^circ$, $sin 52^circ 30’$, $cot 82^circ$, $tan 80^circ$.
Lời giải:
Đây là dạng toán cơ bản khi học về tỷ số lượng giác của góc nhọn, vận dụng tính chất lượng giác của hai góc phụ nhau:
- $sin 60^circ = cos (90^circ – 60^circ) = cos 30^circ$
- $cos 75^circ = sin (90^circ – 75^circ) = sin 15^circ$
- $sin 52^circ 30′ = cos (90^circ – 52^circ 30′) = cos 37^circ 30’$
- $cot 82^circ = tan (90^circ – 82^circ) = tan 8^circ$
- $tan 80^circ = cot (90^circ – 80^circ) = cot 10^circ$
Trên đây là các thông tin tổng quan được chúng tôi tổng hợp lại về hệ thức lượng trong tam giác vuông và hướng dẫn một số lời giải chi tiết những bài tập liên quan. Hy vọng rằng qua những thông tin hữu ích trên có thể giúp bạn trong quá trình học bài và làm bài tập nhé.