Đường Cao Tam Giác Vuông: Định Nghĩa, Công Thức Và Ví Dụ Chi Tiết

Đường cao trong tam giác là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học phẳng, đặc biệt là đối với tam giác vuông. Việc nắm vững định nghĩa, các công thức liên quan đến đường Cao Tam Giác Vuông không chỉ giúp giải quyết hiệu quả các bài toán hình học mà còn là nền tảng cho nhiều kiến thức toán học nâng cao. Bài viết này sẽ đi sâu vào định nghĩa, các công thức tính toán và ví dụ minh họa cụ thể cho đường cao trong tam giác vuông, đồng thời mở rộng sang các loại tam giác khác để bạn có cái nhìn toàn diện hơn về khái niệm này.

I. Định Nghĩa Đường Cao Trong Tam Giác Và Các Tính Chất Quan Trọng

Trong hình học, đường cao của một tam giác là đoạn thẳng được kẻ từ một đỉnh của tam giác xuống cạnh đối diện (hoặc đường thẳng chứa cạnh đối diện) và vuông góc với cạnh đó. Điểm mà đường cao cắt cạnh đối diện được gọi là chân đường cao, và cạnh đối diện đó được gọi là đáy ứng với đường cao. Độ dài của đường cao chính là khoảng cách từ đỉnh đến đáy.

Mỗi tam giác đều có ba đường cao, tương ứng với ba đỉnh và ba cạnh đáy. Một tính chất đặc biệt của ba đường cao là chúng luôn cùng đi qua một điểm. Điểm này được gọi là trực tâm của tam giác. Tùy thuộc vào loại tam giác, trực tâm có thể nằm bên trong, bên ngoài hoặc nằm trên một đỉnh của tam giác (đối với tam giác vuông). Để hiểu rõ hơn về các khái niệm hình học cơ bản, bạn có thể tham khảo thêm kiến thức hình học cơ bản.

II. Công Thức Tính Đường Cao Trong Tam Giác Vuông

Trong tam giác vuông, đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền đóng vai trò đặc biệt quan trọng, liên quan mật thiết đến các hệ thức lượng trong tam giác vuông. Đây là phần kiến thức cốt lõi và thường xuyên xuất hiện trong các bài toán.

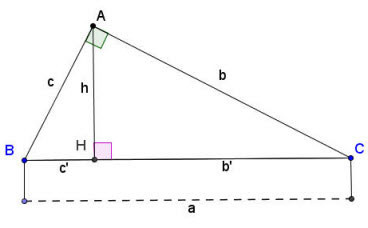Minh họa tam giác vuông ABC với đường cao AH và các cạnh

Giả sử chúng ta có tam giác vuông ABC vuông tại A, đường cao AH kẻ từ A xuống cạnh huyền BC (như hình vẽ trên). Các cạnh góc vuông là AB (ký hiệu c) và AC (ký hiệu b), cạnh huyền là BC (ký hiệu a). H là chân đường cao trên cạnh huyền BC, chia BC thành hai đoạn BH (ký hiệu c’) và CH (ký hiệu b’). Độ dài đường cao là AH (ký hiệu h).

Dưới đây là các công thức tính cạnh và đường cao trong tam giác vuông:

1. Định lý Pytago: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông:
   a² = b² + c² (tức là BC² = AC² + AB²)
2. Hệ thức về cạnh góc vuông và hình chiếu: Bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó lên cạnh huyền:
   b² = a.b' (tức là AC² = BC.CH)
   c² = a.c' (tức là AB² = BC.BH)
3. Hệ thức về đường cao và hình chiếu: Bình phương đường cao ứng với cạnh huyền bằng tích của hai hình chiếu của hai cạnh góc vuông lên cạnh huyền:
   h² = b'.c' (tức là AH² = BH.CH)
4. Hệ thức về đường cao và diện tích: Tích của cạnh huyền và đường cao tương ứng bằng tích của hai cạnh góc vuông (công thức diện tích tam giác vuông):
   a.h = b.c (tức là BC.AH = AB.AC)
5. Hệ thức nghịch đảo bình phương đường cao: Nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng nghịch đảo bình phương hai cạnh góc vuông:
   1/h² = 1/b² + 1/c² (tức là 1/AH² = 1/AB² + 1/AC²)

Việc nắm vững những hệ thức này giúp chúng ta dễ dàng tính toán các yếu tố còn thiếu trong tam giác vuông. Đây là những kiến thức có tầm quan trọng của việc học trong chương trình toán phổ thông.

Ví dụ 1: Tính BC, AC, AH trong tam giác vuông

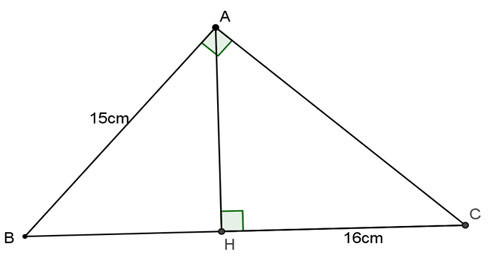Ví dụ 1 về tam giác vuông ABC có đường cao AH

Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.

Giải:

Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AC² = CH.BC = 16.BC

Theo định lí Pythagore cho tam giác ABC vuông tại A, ta có:
AB² + AC² = BC²
↔ 15² + 16.BC = BC²
↔ BC² - 16.BC - 225 = 0

Đây là phương trình bậc hai với ẩn BC. Sử dụng công thức nghiệm hoặc phân tích thành nhân tử:
↔ BC² - 25.BC + 9.BC - 225 = 0
↔ BC(BC - 25) + 9(BC - 25) = 0
↔ (BC - 25)(BC + 9) = 0
↔ BC = 25 hoặc BC = -9 (loại vì độ dài không thể âm).
Vậy BC = 25 cm.

Tính AC:
AC² = 16.BC = 16.25 = 400
→ AC = √400 = 20 (cm)

Tính AH:
Xét tam giác vuông ABC, ta có hệ thức AH.BC = AB.AC
→ AH = (AB.AC) / BC = (15.20) / 25 = 12 (cm)

Vậy BC = 25 cm; AC = 20 cm; AH = 12 cm.

Ví dụ 2: Ứng dụng trong bài toán đường trung trực

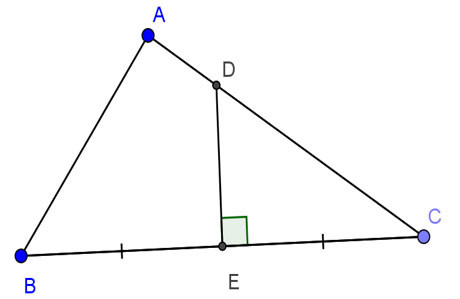Ví dụ 2 về tam giác vuông ABC và đường trung trực của BC

Cho tam giác ABC vuông tại A, AB = 24cm, AC = 32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.

Giải:

Xét tam giác vuông ABC, áp dụng định lý Pytago ta có:
BC² = AB² + AC²
BC² = 24² + 32² = 576 + 1024 = 1600
BC = √1600 = 40 (cm)

Vì DE là đường trung trực của BC nên E là trung điểm của BC.
EC = BC : 2 = 40 : 2 = 20 (cm)

Xét tam giác vuông ACB và tam giác vuông ECD có:
Góc ∠ A = ∠ E = 90°
Góc ∠ C chung
→ Tam giác ACB ~ tam giác ECD (theo trường hợp góc-góc)

Từ tính chất hai tam giác đồng dạng, ta có tỉ lệ các cạnh tương ứng:
AC / EC = AB / ED
→ ED = (AB.EC) / AC = (24.20) / 32 = 480 / 32 = 15 (cm)

Vậy ED = 15 cm.

III. Công Thức Tính Đường Cao Trong Các Loại Tam Giác Khác

Mặc dù trọng tâm bài viết là đường cao tam giác vuông, việc tìm hiểu các công thức đường cao trong các loại tam giác khác cũng rất hữu ích để có cái nhìn tổng quát.

1. Đường cao trong tam giác thường

Đối với tam giác thường ABC với các cạnh có độ dài a, b, c, và p là nửa chu vi (p = (a+b+c)/2), ta có thể sử dụng công thức Heron để tính diện tích S, sau đó suy ra độ dài đường cao.

Công thức diện tích S:
S = √[p(p-a)(p-b)(p-c)]

Từ công thức diện tích S = ½ * đáy * chiều cao, ta suy ra công thức tính đường cao h_a ứng với cạnh a:
h_a = (2 * S) / a
Vậy, h_a = 2 * √[p(p-a)(p-b)(p-c)] / a

Với a, b, c là độ dài các cạnh; h_a là đường cao được kẻ từ đỉnh A xuống cạnh BC; p là nửa chu vi.

Ví dụ:

Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH kẻ từ A cắt BC tại H và tính diện tích ABC.

Giải:

Nửa chu vi tam giác: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8 (cm)

Diện tích tam giác ABC theo công thức Heron:
S = √[8(8-4)(8-7)(8-5)] = √[8.4.1.3] = √96 = 4√6 (cm²)
Hoặc dùng công thức Heron đã biến đổi cho đường cao:

AH = 2 * S / BC = (2 * 4√6) / 7 = 8√6 / 7 (cm)

Lưu ý: Ví dụ gốc có vẻ đã nhầm lẫn trong ký hiệu công thức và kết quả tính toán. Kết quả tính toán AH và S_ABC trong ví dụ gốc không khớp với công thức Heron nếu p-AB, p-AC, p-BC thay cho p-a, p-b, p-c. Tôi sẽ điều chỉnh kết quả theo công thức chuẩn.

Theo tính toán chính xác:
S_ABC = 4√6 cm² ≈ 9.798 cm²
AH = (8√6)/7 cm ≈ 2.799 cm

2. Đường cao trong tam giác đều

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng 60°. Đường cao trong tam giác đều cũng là đường trung tuyến, đường phân giác và đường trung trực.

Giả sử tam giác đều ABC có độ dài cạnh bằng a. Đường cao h được tính bằng công thức:

h = (a√3) / 2

Trong đó:

• h là đường cao của tam giác đều
• a là độ dài cạnh của tam giác đều

3. Đường cao trong tam giác cân

Tam giác cân là tam giác có hai cạnh bên bằng nhau. Đường cao kẻ từ đỉnh đối diện với cạnh đáy sẽ đồng thời là đường trung tuyến, đường phân giác và đường trung trực của cạnh đáy.

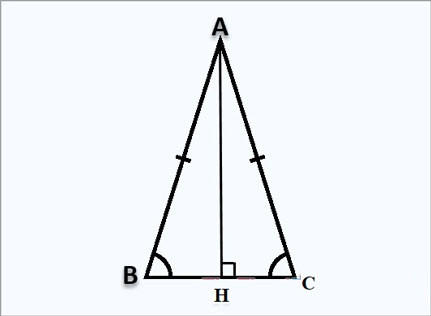Minh họa tam giác cân ABC với đường cao AH

Giả sử tam giác ABC cân tại A, đường cao AH vuông góc tại H trên cạnh BC.
Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến, suy ra H là trung điểm của BC.
→ HB = HC = ½BC

Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H, ta có:
AH² + BH² = AB²
→ AH² = AB² − BH²

Để tính đường cao ứng với cạnh bên, chúng ta cần sử dụng công thức diện tích hoặc hệ thức lượng phức tạp hơn một chút. Khám phá những khám phá và sáng tạo trong việc giải toán có thể mang lại nhiều điều thú vị.

Ví dụ: Cho Δ ABC cân tại A có BC = 30(cm), đường cao AH = 20(cm). Tính đường cao ứng với cạnh bên của tam giác cân đó.

Giải:

Xét Δ ABC cân tại A có BC = 30(cm).
Do AH là đường cao đồng thời là đường trung tuyến → BH = CH = 15(cm).

Áp dụng định lý Pytago trong tam giác vuông ABH:
AB² = AH² + BH² = 20² + 15² = 400 + 225 = 625
AB = √625 = 25 (cm)
Vì Δ ABC cân tại A nên AC = AB = 25 cm.

Kẻ đường cao BK ứng với cạnh bên AC. Giờ ta cần tính BK.
Ta có công thức diện tích tam giác: S_ABC = ½ * AH * BC
S_ABC = ½ * 20 * 30 = 300 (cm²)

Mặt khác, ta cũng có thể tính diện tích bằng đường cao BK và cạnh đáy AC:
S_ABC = ½ * BK * AC
300 = ½ * BK * 25
→ BK = (2 * 300) / 25 = 600 / 25 = 24 (cm)

Vậy đường cao ứng với cạnh bên của tam giác cân đó là 24 cm.

Kết luận

Đường cao trong tam giác, đặc biệt là đường cao tam giác vuông, là một khái niệm hình học cơ bản nhưng có ứng dụng rộng rãi. Nắm vững định nghĩa, các hệ thức lượng và công thức tính đường cao cho từng loại tam giác sẽ trang bị cho bạn một nền tảng vững chắc để giải quyết các bài toán từ đơn giản đến phức tạp. Từ Định lý Pytago đến hệ thức lượng, mỗi công thức đều mở ra những cách tiếp cận khác nhau để tìm ra các yếu tố còn thiếu trong tam giác.

Hãy luyện tập thường xuyên và áp dụng linh hoạt các công thức này để củng cố kiến thức và phát triển kỹ năng giải toán của mình. Việc tìm hiểu sâu sắc và ứng dụng kiến thức sẽ mang lại những ý nghĩa quan trọng không chỉ trong học tập mà còn trong nhiều lĩnh vực khác của cuộc sống. Xây dựng một nền tảng kiến thức vững chắc là điều cần thiết để đạt được những giá trị vững bền trong mọi hành trình.