Hình tứ giác là một trong những hình học cơ bản xuất hiện thường xuyên trong chương trình toán tiểu học, đặc biệt là ở các khối lớp 3 và 4. Việc nắm vững Cách Tính Chu Vi Hình Tứ Giác không chỉ giúp các em học sinh giải quyết tốt các bài tập trên lớp mà còn là nền tảng quan trọng cho những kiến thức hình học phức tạp hơn sau này. Bài viết này của CÔNG TY TNHH MÔI TRƯỜNG HSE sẽ cung cấp cho bạn một cái nhìn toàn diện về chu vi hình tứ giác, từ công thức tổng quát đến cách áp dụng cho từng loại hình cụ thể, cùng với các dạng bài tập và bí quyết giúp bé học hiệu quả. Chu vi hình tứ giác, dù là hình bất kỳ hay hình đặc biệt, đều có công thức tính rất đơn giản và dễ hiểu, chỉ cần cộng tổng độ dài bốn cạnh của nó.
Chu vi hình tứ giác là gì và công thức tính tổng quát
Chu vi của một hình tứ giác chính là tổng độ dài của tất cả các cạnh bao quanh hình đó. Nói cách khác, nếu bạn có một hình tứ giác với bốn cạnh, chu vi của nó sẽ là quãng đường bạn đi hết một vòng quanh hình.
Công thức tính chu vi hình tứ giác bất kỳ bằng tổng độ dài bốn cạnh của nó. Muốn tính chu vi của hình tứ giác, bạn chỉ cần cộng tổng độ dài của cả 4 cạnh với nhau.
Công thức tổng quát:
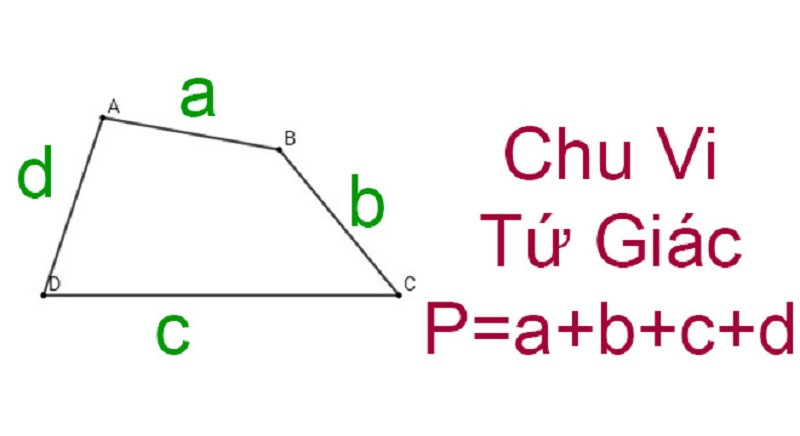
Nếu một tứ giác có độ dài các cạnh là a, b, c và d, thì chu vi của tứ giác đó sẽ là:
P = a + b + c + d (đơn vị tính)
Trong đó:
- P: Chu vi hình tứ giác
- a, b, c, d: Độ dài 4 cạnh của tứ giác.
Ví dụ: Cho tứ giác EFGH có độ dài các cạnh lần lượt là EF = 7cm, FG = 4cm, GH = 9cm và HE = 6cm. Chu vi của tứ giác EFGH sẽ là:
P = 7 + 4 + 9 + 6 = 26 (cm)
Lưu ý quan trọng: Công thức này áp dụng cho mọi loại tứ giác, bất kể có hay không các cạnh bằng nhau. Nói cách khác, không cần thiết phải biết tứ giác là hình vuông, hình chữ nhật, hình thoi hay hình thang; chỉ cần biết độ dài của cả bốn cạnh là đủ để tính chu vi. Điều này làm cho việc tính toán trở nên cực kỳ linh hoạt và dễ dàng cho học sinh.
Các phương pháp tính chu vi hình tứ giác theo từng loại
Hình tứ giác có thể được chia thành hai dạng chính: tứ giác thường và tứ giác đặc biệt. Dưới đây là công thức tính chu vi cho từng dạng.
Tính chu vi tứ giác thường
Với hình tứ giác thường, khi tính chu vi sẽ bằng tổng độ dài 4 cạnh, tức là:
P = a + b + c + d (đơn vị tính)
Trong đó:
- P: Chu vi hình tứ giác
- a, b, c, d: Độ dài 4 cạnh của tứ giác.
Ví dụ: Cho tứ giác ABCD có độ dài 4 cạnh AB = 3cm, BC = 5cm, CD = 4 cm, AD = 6cm.
Chu vi tứ giác ABCD:
P = 3 + 5 + 4 + 6 = 18 (cm)
Công thức tính chu vi các hình tứ giác đặc biệt
Với các hình tứ giác đặc biệt bao gồm: Hình vuông, hình thoi, hình chữ nhật, hình bình hành, hình thang. Việc tính chu vi của các hình này khá đơn giản và có thể tối ưu hơn công thức tổng quát. Đôi khi, những yếu tố tưởng chừng nhỏ bé như việc chọn một hình nền iphone 15 pro max 4k đẹp cũng có thể tạo cảm hứng học tập cho các em, giúp các em thấy toán học cũng có thể đẹp và thú vị như những thứ xung quanh.
- Chu vi hình thang có độ dài 4 cạnh là a, b, c, d là: P = a + b + c + d (Tương tự tứ giác thường, vì hình thang chỉ có một cặp cạnh song song, không nhất thiết có các cạnh khác bằng nhau).
- Chu vi hình bình hành, hình chữ nhật là: P = 2.(a + b) (Vì các cạnh đối diện bằng nhau. Trong đó ‘a’ là chiều dài và ‘b’ là chiều rộng/cạnh liền kề).
- Chu vi hình vuông, hình thoi là: P = 4.a (Vì tất cả 4 cạnh đều có độ dài bằng nhau. Trong đó ‘a’ là độ dài một cạnh).
Trong đó:
- P: Chu vi hình tứ giác đặc biệt
- a, b, c, d: Độ dài cạnh của hình tứ giác (tùy thuộc vào loại hình mà các cạnh có thể bằng nhau hoặc khác nhau).
Ví dụ minh họa cách tính chu vi hình tứ giác cho học sinh tiểu học (lớp 3, 4)
Việc áp dụng các công thức vào ví dụ cụ thể giúp học sinh dễ hình dung và ghi nhớ kiến thức lâu hơn. Dưới đây là một số ví dụ thực tế.
Ví dụ 1: Tính chu vi hình thang
Cho hình thang có các cạnh lần lượt là 8cm, 5cm, 10cm và 6cm.
Chu vi hình thang là: P = 8 + 5 + 10 + 6 = 29 (cm).
Ví dụ 2: Tính chu vi hình chữ nhật
Một hình chữ nhật có chiều dài 15m và chiều rộng 8m.
Chu vi hình chữ nhật là: P = 2 (15 + 8) = 2 23 = 46 (m).
Ví dụ 3: Tính chu vi hình vuông
Một mảnh vườn hình vuông có cạnh dài 12 mét.
Chu vi mảnh vườn là: P = 4 * 12 = 48 (m).
Các dạng bài tập phổ biến về chu vi hình tứ giác
Đối với các bé học cấp 1, kiến thức về chu vi hình tứ giác thường ở dạng cơ bản. Vậy nên, sẽ có những dạng bài tập liên quan sau đây:
 Các dạng bài tập đa dạng về cách tính chu vi hình tứ giác cho học sinh
Các dạng bài tập đa dạng về cách tính chu vi hình tứ giác cho học sinh
Dạng 1: Tính chu vi tứ giác khi biết độ dài các cạnh
Đây là dạng bài tập cơ bản nhất, khi đề bài sẽ cho thông tin dữ kiện về độ dài các cạnh của tứ giác và yêu cầu bé tính chu vi hình tương ứng. Vậy nên, các em chỉ cần áp dụng công thức tính chu vi P = a + b + c + d để tính toán chính xác. Giống như cách làm bún thịt nướng cần tuân thủ từng bước công thức để có kết quả ngon miệng, việc giải toán cũng yêu cầu theo đúng công thức để đạt đáp án chính xác.
Ví dụ: Tính chu vi tứ giác có các cạnh sau:
- 5dm, 3dm, 6dm, 4dm
- 3cm, 5cm, 4cm, 3,5cm
Giải:
Áp dụng công thức tính chu vi ta có:
- P = 5 + 3 + 6 + 4 = 18dm
- P = 3 + 5 + 4 + 3,5 = 15,5cm
Dạng 2: Cho chu vi, tìm độ dài cạnh
Bài tập này sẽ ngược lại so với dạng 1, khi đề bài sẽ cho chu vi hình tứ giác và yêu cầu tính độ dài cạnh. Nên cũng sẽ dựa vào công thức P = a + b + c + d để tính được cạnh tương ứng. Đôi khi, cuộc sống cũng có những mẹo vặt biết có thai dựa trên những dấu hiệu ngược lại, tương tự như việc suy luận ngược từ chu vi để tìm cạnh.
Ví dụ: Hình tứ giác MNPQ có chu vi 52cm, biết tổng độ dài hai cạnh MN và NP bằng 21cm. Tìm tổng độ dài của hai cạnh PQ và QM.
Giải:
Ta có chu vi tứ giác MNPQ: P = MN + NP + PQ + QM = 52
Mà MN + NP = 21
P = 21 + (PQ + QM) = 52
Tổng độ dài của hai cạnh PQ và QM là: PQ + QM = 52 – 21 = 31 (cm)
Đáp số: 31cm
Dạng 3: Tính chu vi hình tứ giác đặc biệt
Ở dạng bài tập này sẽ cho một hình tứ giác cụ thể như hình vuông, hình chữ nhật,… kèm theo các dữ kiện về cạnh, yêu cầu tính chu vi của hình đó. Nên tùy thuộc vào từng hình sẽ áp dụng công thức tương ứng để tính toán chính xác.
Ví dụ: Cho mảnh đất hình vuông có độ dài cạnh tương ứng là 12cm. Tính chu vi của mảnh đất đó.
Giải:
Chu vi mảnh đất hình vuông tương ứng là: P = a x 4 = 12 x 4 = 48cm.
Đáp số: 48cm
Bài luyện tập cách tính chu vi hình tứ giác thực hành (Toán lớp 3, 4)
Dưới đây sẽ là tổng hợp một số bài tập về tính chu vi của hình tứ giác để bé có thể áp dụng những kiến thức trên và thực hành:
 Bài luyện tập về cách tính chu vi hình tứ giác dành cho cấp tiểu học
Bài luyện tập về cách tính chu vi hình tứ giác dành cho cấp tiểu học
- Tính chu vi hình tứ giác ABCD biết độ dài các cạnh là: AB = 6cm, BC = 8cm, CD = 7cm, DA = 9cm.
- Một hình chữ nhật có chiều dài 20cm và chiều rộng 12cm. Tính chu vi hình chữ nhật đó.
- Hình thoi có cạnh dài 10dm. Hỏi chu vi hình thoi là bao nhiêu?
- Tính chu vi hình tứ giác MNPQ biết MN = 5dm, NP = 7dm, PQ = 9dm và QM = 4dm.
- Một hình bình hành có một cạnh 15m và cạnh liền kề là 10m. Tính chu vi hình bình hành.
- Nếu chu vi một hình vuông là 36cm, hỏi độ dài một cạnh của hình vuông đó là bao nhiêu?
Bí quyết giúp bé ghi nhớ cách tính chu vi tứ giác hiệu quả
Công thức tính chu vi của hình tứ giác không chỉ để giải bài tập toán trong chương trình học tập mà còn được ứng dụng trong thực tế để giải quyết các công việc đặc thù như xây dựng, thiết kế,… Đối với các bé học cấp 1, đặc biệt là các bạn lớp 3, 4, các con cần nắm chắc phần kiến thức cơ bản này để học tốt phần tính toán ở lớp trên. Một số phương pháp ba mẹ nên áp dụng đó là:
Tạo sự hứng thú khi học toán cho bé cùng Monkey Math
Bởi vì toán học là một bộ môn chỉ xoay quanh số, phép tính và hình học. Cùng với lượng kiến thức khá nhiều, nên đòi hỏi phải có phương pháp dạy phù hợp thì bé mới có sự hứng thú và tiếp thu kiến thức hiệu quả. Sự phát triển tư duy từ sớm, thậm chí từ giai đoạn tiền thai giáo với nhạc thai giáo 3 tháng đầu, đã cho thấy tầm quan trọng của việc kích thích trí não. Do đó, việc học toán cũng cần được tiếp cận một cách sáng tạo để duy trì sự hứng thú.
Trường hợp nếu bố mẹ không có nhiều thời gian để hỗ trợ bé học tập, hay không tự tin về việc truyền thụ kiến thức của mình có thể lựa chọn Monkey Math để đồng hành cùng với bé. Đây là một trong những ứng dụng dạy học toán tiếng Anh được hàng triệu bố mẹ tin dùng.
 Phương pháp học toán thú vị với ứng dụng Monkey Math
Phương pháp học toán thú vị với ứng dụng Monkey Math
Điểm đặc biệt của Monkey Math chính là hướng dẫn dạy bé học toán dựa trên nhiều phương pháp khác nhau. Điển hình như:
- Áp dụng phương pháp dạy học tích cực: Kích thích sự sáng tạo, con tích cực đặt câu hỏi để hiểu tận gốc vấn đề được đưa ra trong Toán học.
- Học thông qua trò chơi: Vừa chơi vừa học mà hiệu quả vượt bậc. Con hứng thú, tự giác học không cần ba mẹ nhắc nhở.
- Học với sách bài tập bổ trợ: Giúp con phát triển các kỹ năng vận động tinh và vận động thô thông qua việc giải quyết các bài toán trong thực tế.
Nội dung chương trình học sẽ dựa trên hơn 60 chủ đề thuộc 7 chuyên đề toán học lớn giúp trẻ dễ dàng nắm bắt các khái niệm toán học, trong đó có cả kiến thức về hình học. Để qua đó sẽ giúp xây dựng nền tảng Toán học & hỗ trợ việc học trên lớp hiệu quả, cũng như giúp con phát triển đồng bộ tư duy & ngôn ngữ giúp con học giỏi cả toán và tiếng Anh.
Đăng ký tài khoản Ngay Tại Đây để nhận ưu đãi lên đến 40% và nhiều tài liệu học tập miễn phí!
Đảm bảo bé nắm vững kiến thức cơ bản về chu vi hình tứ giác
Để có thể giải bài tập hình tứ giác và ứng dụng chính xác trong thực tế, đòi hỏi bé phải nắm vững các kiến thức cơ bản liên quan tới chúng. Bao gồm: Thế nào là hình tứ giác, các loại hình tứ giác, công thức tính chu vi, các dạng bài tập,…
Để làm được điều này, bố mẹ nên đồng hành học cùng bé, thường xuyên đặt ra các câu hỏi liên quan để xem bé nhớ kiến thức tới đâu, kiểm tra sách vở,… Điều này sẽ giúp bạn biết được năng lực học của con, cùng với việc biết được kiến thức nào bé còn yếu để có thể củng cố kịp thời. Đôi khi, những chi tiết tưởng chừng nhỏ bé, như một giấc mơ thấy đồng hồ đeo tay cũng có thể là một dấu hiệu để ta suy ngẫm, tương tự như việc cha mẹ cần chú ý đến từng dấu hiệu nhỏ trong quá trình học tập của con.
Cùng bé thực hành, luyện tập nhiều hơn
Trong quá trình học tập của bé, bố mẹ nên tạo điều kiện để con được thực hành thường xuyên từ việc làm nhiều bài tập liên quan trong SGK, internet, luyện đề thi, tìm hiểu thêm nhiều kiến thức mới nâng cao, tự tổ chức các cuộc thi nhỏ cho bé, học toán thông qua trò chơi…
Chính việc được thực hành nhiều hơn, bé sẽ dễ dàng tiếp thu kiến thức, cũng như có sự hứng thú hơn khi học toán bớt nhàm chán.
Kết luận
Trên đây là những kiến thức chi tiết giúp bạn và các bé hiểu rõ hơn về cách tính chu vi hình tứ giác. Nhìn chung, kiến thức cơ bản này sẽ có những phần dễ, phần khó, chỉ cần nắm vững những thông tin mà chúng tôi đã chia sẻ sẽ giúp trẻ chinh phục được các bài tập một cách hiệu quả nhất. Việc học tập là một hành trình dài, đòi hỏi sự kiên trì và phương pháp đúng đắn. Hãy cùng con khám phá thế giới toán học đầy thú vị và xây dựng nền tảng vững chắc cho tương lai. Chúc các bé có những giờ học tập vui vẻ và thành công!
