Trong thế giới hình học phẳng, tam giác luôn là một trong những hình cơ bản nhưng chứa đựng vô vàn tính chất thú vị và ứng dụng rộng rãi. Và trong số các yếu tố đặc biệt của tam giác, đường cao đóng vai trò cực kỳ quan trọng, không chỉ giúp xác định diện tích mà còn là chìa khóa để giải quyết nhiều bài toán phức tạp. Bạn đang tìm kiếm một định nghĩa rõ ràng, các công thức tính toán chính xác hay muốn hiểu sâu hơn về những ứng dụng của đường Cao Trong Tam Giác? Hãy cùng CÔNG TY TNHH MÔI TRƯỜNG HSE khám phá chi tiết về đường cao trong tam giác qua bài viết chuyên sâu này, từ đó củng cố kiến thức và tự tin hơn với môn hình học.
Đường Cao Trong Tam Giác Là Gì? Định Nghĩa Chi Tiết
Đường cao trong tam giác là một đoạn thẳng được kẻ từ một đỉnh của tam giác xuống cạnh đối diện (hoặc đường thẳng chứa cạnh đối diện) và vuông góc với cạnh đó. Điểm mà đường cao cắt cạnh đối diện được gọi là chân đường cao. Độ dài của đường cao chính là khoảng cách từ đỉnh đến cạnh đáy tương ứng.
Mỗi tam giác đều có ba đường cao, tương ứng với ba đỉnh và ba cạnh đáy. Ví dụ, trong tam giác ABC, chúng ta có:
- Đường cao từ đỉnh A xuống cạnh BC.
- Đường cao từ đỉnh B xuống cạnh AC.
- Đường cao từ đỉnh C xuống cạnh AB.
Khái niệm đường cao là nền tảng để hiểu về các tính chất hình học khác và là công cụ thiết yếu để tính toán diện tích tam giác.
Tổng Hợp Các Công Thức Tính Đường Cao Trong Tam Giác
Việc tính toán độ dài đường cao phụ thuộc vào loại tam giác và các thông số đã biết. Dưới đây là các công thức phổ biến nhất cho từng trường hợp.
Cách Tính Đường Cao Trong Tam Giác Thường
Đối với một tam giác thường (không có tính chất đặc biệt như cân, đều hay vuông), chúng ta có thể sử dụng công thức Heron để tính diện tích, sau đó suy ra độ dài đường cao.
Công thức Heron giúp tính diện tích S của tam giác khi biết độ dài ba cạnh a, b, c:
$S = sqrt{p(p-a)(p-b)(p-c)}$
Trong đó:
- a, b, c là độ dài ba cạnh của tam giác.
- p là nửa chu vi của tam giác: $p = frac{a+b+c}{2}$
Sau khi có diện tích S, đường cao $h_a$ (kẻ từ đỉnh A xuống cạnh a) được tính bằng công thức:
$h_a = frac{2S}{a}$
Tương tự, đường cao $h_b = frac{2S}{b}$ và $h_c = frac{2S}{c}$.
Ví dụ: Cho tam giác ABC có cạnh AB = 4 cm, BC = 7 cm, AC = 5 cm. Tính đường cao AH (kẻ từ A xuống BC) và diện tích tam giác ABC.
Giải:
- Tính nửa chu vi p:
$p = frac{AB + BC + AC}{2} = frac{4 + 7 + 5}{2} = frac{16}{2} = 8 text{ (cm)}$ - Tính diện tích S của tam giác ABC theo công thức Heron:
$S = sqrt{p(p-AB)(p-BC)(p-AC)} = sqrt{8(8-4)(8-7)(8-5)} = sqrt{8 cdot 4 cdot 1 cdot 3} = sqrt{96} = 4sqrt{6} text{ (cm}^2text{)}$ - Tính đường cao AH (ứng với cạnh BC):
$AH = frac{2S}{BC} = frac{2 cdot 4sqrt{6}}{7} = frac{8sqrt{6}}{7} text{ (cm)}$
Vậy, diện tích tam giác ABC là $4sqrt{6} text{ cm}^2$ và đường cao AH là $frac{8sqrt{6}}{7} text{ cm}$.
Công Thức Tính Đường Cao Trong Tam Giác Đều
Tam giác đều là loại tam giác có ba cạnh bằng nhau và ba góc bằng nhau (đều bằng $60^circ$). Trong tam giác đều, ba đường cao cũng có độ dài bằng nhau và đồng thời là đường trung tuyến, đường phân giác của các góc, và đường trung trực của các cạnh.
Nếu tam giác đều có độ dài cạnh là a, thì đường cao h của nó được tính bằng công thức:
$h = a frac{sqrt{3}}{2}$
Ví dụ: Cho tam giác đều có cạnh bằng 6 cm. Tính độ dài đường cao.
Giải:
Áp dụng công thức, ta có:
$h = 6 frac{sqrt{3}}{2} = 3sqrt{3} text{ (cm)}$
Đường Cao Trong Tam Giác Vuông: Công Thức Và Ví Dụ Áp Dụng
Trong tam giác vuông, đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền có những tính chất đặc biệt và thường được tính thông qua các hệ thức lượng.
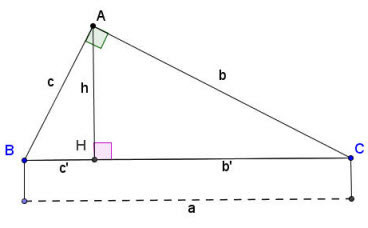Hình ảnh minh họa đường cao trong tam giác vuông với các cạnh và ký hiệu
Giả sử tam giác ABC vuông tại A, đường cao AH kẻ từ A xuống cạnh huyền BC. Gọi độ dài các cạnh là BC = a (cạnh huyền), AC = b, AB = c. Gọi BH = b’ và CH = c’ là hình chiếu của các cạnh góc vuông lên cạnh huyền. Đường cao AH = h.
Các hệ thức lượng cơ bản trong tam giác vuông liên quan đến đường cao bao gồm:
- Định lý Pytago: $a^2 = b^2 + c^2$
- Quan hệ giữa cạnh góc vuông và hình chiếu: $b^2 = a cdot b’$ và $c^2 = a cdot c’$
- Quan hệ giữa đường cao và các cạnh góc vuông: $a cdot h = b cdot c$ (Diện tích tam giác vuông có thể tính bằng $frac{1}{2}bc$ hoặc $frac{1}{2}ah$)
- Quan hệ giữa đường cao và hình chiếu: $h^2 = b’ cdot c’$
- Nghịch đảo bình phương đường cao: $frac{1}{h^2} = frac{1}{b^2} + frac{1}{c^2}$
Đây là những công thức rất hữu ích khi bạn cần tìm đường cao trong tam giác vuông hoặc các yếu tố khác liên quan.
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
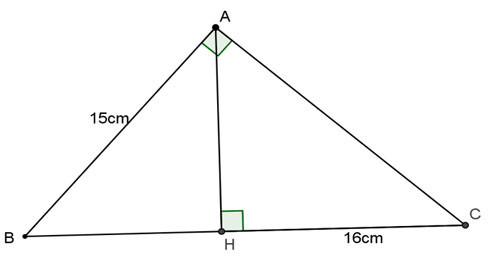Ví dụ minh họa tam giác ABC vuông tại A với đường cao AH
Giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC vuông tại A:
- Ta có: $AC^2 = CH cdot BC$ (vì AC là cạnh góc vuông, CH là hình chiếu của AC lên cạnh huyền BC).
$AC^2 = 16 cdot BC$ (1) - Theo định lý Pytago trong tam giác ABC: $AB^2 + AC^2 = BC^2$
Thay (1) vào, ta có: $15^2 + 16 cdot BC = BC^2$
$225 + 16 cdot BC = BC^2$
$BC^2 – 16 cdot BC – 225 = 0$ - Giải phương trình bậc hai:
$BC^2 – 25 cdot BC + 9 cdot BC – 225 = 0$
$BC(BC – 25) + 9(BC – 25) = 0$
$(BC – 25)(BC + 9) = 0$
Suy ra $BC = 25$ (cm) hoặc $BC = -9$ (loại vì độ dài không thể âm). - Tính AC: Thay BC = 25 vào (1):
$AC^2 = 16 cdot 25 = 400 Rightarrow AC = sqrt{400} = 20 text{ (cm)}$ - Tính AH: Áp dụng hệ thức $AH cdot BC = AB cdot AC$:
$AH = frac{AB cdot AC}{BC} = frac{15 cdot 20}{25} = frac{300}{25} = 12 text{ (cm)}$
Vậy, BC = 25 cm, AC = 20 cm, AH = 12 cm. Những kiến thức này rất quan trọng để hiểu rõ về đường cao tam giác vuông.
Công Thức Tính Đường Cao Trong Tam Giác Cân
Tam giác cân là tam giác có hai cạnh bên bằng nhau. Đường cao kẻ từ đỉnh đối diện với cạnh đáy xuống cạnh đáy có một tính chất đặc biệt: nó đồng thời là đường trung tuyến, đường phân giác của góc ở đỉnh và đường trung trực của cạnh đáy.
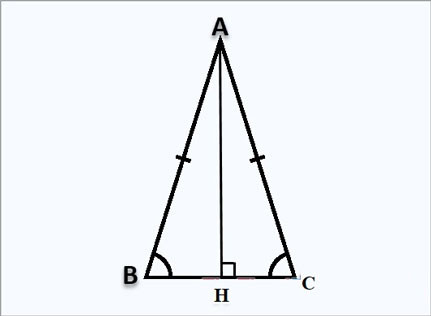Hình ảnh minh họa đường cao trong tam giác cân
Giả sử tam giác ABC cân tại A, đường cao AH kẻ từ A xuống cạnh đáy BC. Vì AH là đường cao và cũng là đường trung tuyến, nên H là trung điểm của BC, tức là $HB = HC = frac{1}{2}BC$.
Để tính đường cao AH, ta áp dụng định lý Pytago trong tam giác vuông ABH (hoặc ACH):
$AH^2 + BH^2 = AB^2$
Từ đó suy ra:
$AH^2 = AB^2 – BH^2$
$AH = sqrt{AB^2 – BH^2}$
Ví dụ: Cho tam giác ABC cân tại A có BC = 30 cm, đường cao AH = 20 cm. Tính độ dài đường cao ứng với cạnh bên của tam giác cân đó (ví dụ đường cao BK kẻ từ B xuống AC).
Giải:
- Tính BH: Vì tam giác ABC cân tại A, AH là đường cao nên H là trung điểm của BC.
$BH = frac{1}{2}BC = frac{1}{2} cdot 30 = 15 text{ (cm)}$ - Tính cạnh bên AB (hoặc AC) bằng định lý Pytago trong tam giác vuông ABH:
$AB^2 = AH^2 + BH^2 = 20^2 + 15^2 = 400 + 225 = 625$
$AB = sqrt{625} = 25 text{ (cm)}$
Vì tam giác ABC cân tại A, nên $AC = AB = 25 text{ (cm)}$. - Tính diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} cdot AH cdot BC = frac{1}{2} cdot 20 cdot 30 = 300 text{ (cm}^2text{)}$ - Tính đường cao BK ứng với cạnh bên AC:
Ta biết diện tích tam giác cũng có thể tính bằng $S_{ABC} = frac{1}{2} cdot BK cdot AC$.
$300 = frac{1}{2} cdot BK cdot 25$
$BK = frac{2 cdot 300}{25} = frac{600}{25} = 24 text{ (cm)}$
Vậy, đường cao ứng với cạnh bên của tam giác cân là 24 cm.
Tính Chất Ba Đường Cao Của Tam Giác: Khái Niệm Trực Tâm
Một trong những tính chất quan trọng nhất của ba đường cao trong một tam giác là chúng luôn đồng quy tại một điểm duy nhất. Điểm đồng quy này được gọi là trực tâm của tam giác.
Vị trí của trực tâm phụ thuộc vào loại tam giác:
- Trong tam giác nhọn: Trực tâm nằm bên trong tam giác.
- Trong tam giác vuông: Trực tâm trùng với đỉnh góc vuông.
- Trong tam giác tù: Trực tâm nằm bên ngoài tam giác.
Trực tâm là một trong bốn điểm đặc biệt của tam giác (cùng với trọng tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp), mỗi điểm mang một ý nghĩa và ứng dụng riêng biệt trong hình học. Để không nhầm lẫn với các khái niệm khác như trọng tâm của tam giác là gì, bạn cần nắm vững định nghĩa và tính chất của từng loại điểm đặc biệt này.
Tầm Quan Trọng Của Đường Cao Trong Hình Học Và Ứng Dụng Thực Tiễn
Đường cao không chỉ là một yếu tố lý thuyết trong toán học mà còn có nhiều ứng dụng thực tiễn quan trọng:
- Tính toán diện tích: Đây là ứng dụng cơ bản và phổ biến nhất của đường cao. Công thức diện tích tam giác $S = frac{1}{2} cdot text{đáy} cdot text{chiều cao}$ là nền tảng cho nhiều bài toán và ứng dụng thực tế.
- Giải quyết bài toán hình học phức tạp: Đường cao thường được sử dụng làm công cụ phụ trợ để chứng minh các mối quan hệ giữa các cạnh, góc, hoặc để tìm ra các yếu tố khác trong tam giác.
- Trong kiến trúc và kỹ thuật: Khái niệm chiều cao, độ vuông góc là cốt lõi trong thiết kế các cấu trúc, đo đạc khoảng cách và tính toán ổn định. Ví dụ, trong xây dựng mái nhà, tính toán độ cao của đỉnh mái để đảm bảo độ dốc và thoát nước hiệu quả.
- Trong trắc địa và đo đạc địa hình: Đường cao giúp xác định chiều cao của các vật thể, ngọn núi hoặc độ dốc của địa hình.
Việc nắm vững kiến thức về đường cao trong tam giác giúp bạn không chỉ giải quyết tốt các bài tập trên lớp mà còn mở rộng tư duy logic và khả năng ứng dụng toán học vào các tình huống thực tế.
Kết Luận
Qua bài viết này, CÔNG TY TNHH MÔI TRƯỜNG HSE hy vọng bạn đã có cái nhìn toàn diện và sâu sắc hơn về đường cao trong tam giác, từ định nghĩa, các công thức tính cho từng loại tam giác (thường, đều, vuông, cân) cho đến tính chất đồng quy tạo thành trực tâm. Đây là một khái niệm nền tảng nhưng vô cùng quan trọng, không chỉ trong lĩnh vực toán học mà còn trong nhiều ứng dụng thực tiễn.
Việc hiểu rõ và vận dụng linh hoạt các công thức, tính chất của đường cao sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán hình học và nhận ra giá trị của kiến thức này trong cuộc sống. Hãy tiếp tục khám phá và ứng dụng những kiến thức bổ ích này để mở rộng tầm hiểu biết của bạn về thế giới toán học nhé!