Trong cuộc sống hàng ngày, chúng ta dễ dàng bắt gặp vô số đồ vật có hình dạng hình lập phương quen thuộc như khối rubik, thùng carton, hộp quà, hay những viên xúc xắc. Việc hiểu rõ về hình học không gian, đặc biệt là cách tính Diện Tích Toàn Phần Của Hình Lập Phương, không chỉ giúp ích trong các bài toán trên lớp mà còn có ứng dụng thực tế đáng kể trong nhiều lĩnh vực. Bài viết này sẽ cùng bạn đọc ôn tập lại những kiến thức cơ bản nhất về hình lập phương và đi sâu vào công thức tính diện tích xung quanh cũng như diện tích toàn phần của hình lập phương một cách chi tiết, dễ hiểu. Hãy cùng khám phá để nắm vững kiến thức quan trọng này.
Hình Lập Phương Là Gì? Định Nghĩa Và Tính Chất Cơ Bản
Hình lập phương là một trong những khối hình học cơ bản và quan trọng nhất, không chỉ xuất hiện trong sách giáo khoa toán học mà còn có mặt rộng rãi trong kiến trúc, thiết kế và nhiều ngành nghề khác.
Định nghĩa Hình lập phương
Hình lập phương là một dạng hình khối đặc biệt, có ba chiều: chiều dài, chiều rộng và chiều cao đều bằng nhau. Điều này tạo nên sự cân đối hoàn hảo cho khối hình.
- Hình lập phương được cấu tạo từ 6 mặt phẳng, tất cả đều là các hình vuông bằng nhau.
- Nó cũng có thể được định nghĩa là một hình hộp chữ nhật mà tất cả các cạnh đều có độ dài như nhau.
Hình lập phương minh họa với các cạnh và đỉnh rõ ràng
Các tính chất cơ bản của Hình lập phương
Một số tính chất nổi bật giúp phân biệt hình lập phương với các khối hình khác bao gồm:
- Có 8 mặt phẳng đối xứng, thể hiện sự đối xứng cao của hình khối.
- Gồm 12 cạnh có độ dài bằng nhau và 8 đỉnh. Tại mỗi đỉnh, có 3 cạnh gặp nhau.
- Sở hữu 4 đường chéo chính cắt nhau tại một điểm duy nhất, điểm này chính là tâm đối xứng của hình lập phương.
- Đặc biệt, tất cả các đường chéo của khối hình lập phương đều có độ dài bằng nhau.
Những tính chất này là nền tảng để hiểu sâu hơn về cấu trúc và các phép tính liên quan đến hình lập phương. Đối với những ai yêu thích việc tìm hiểu sâu hơn về các kiến thức văn học mang tính biểu tượng, như phân tích bài thơ quê hương, cũng có thể thấy sự hấp dẫn tương tự trong việc khám phá những chi tiết nhỏ làm nên một tổng thể lớn.
Khám Phá Công Thức Tính Diện Tích Toàn Phần Của Hình Lập Phương
Để tính toán kích thước của một vật thể hình lập phương, chúng ta cần nắm vững các công thức tính diện tích xung quanh và diện tích toàn phần của hình lập phương.
Diện tích xung quanh và diện tích toàn phần: Định nghĩa
- Diện tích xung quanh của hình lập phương là tổng diện tích của bốn mặt bên bao quanh khối hình.
- Diện tích toàn phần của hình lập phương là tổng diện tích của tất cả sáu mặt của hình lập phương (bao gồm bốn mặt xung quanh và hai mặt đáy).
Quy tắc và công thức tính
Giả sử hình lập phương có độ dài cạnh là a.
- Để tính diện tích xung quanh của hình lập phương: Ta lấy diện tích của một mặt (là hình vuông) nhân với 4.
Sxq = Diện tích 1 mặt x 4 = (a x a) x 4 - Để tính diện tích toàn phần của hình lập phương: Ta lấy diện tích của một mặt (là hình vuông) nhân với 6.
Stp = Diện tích 1 mặt x 6 = (a x a) x 6
Những công thức này là cực kỳ quan trọng và được áp dụng rộng rãi. Đôi khi, việc tìm kiếm một không gian yên bình để học tập hoặc làm việc hiệu quả cũng quan trọng không kém, giống như việc tìm một quán cafe đẹp ở huế có thể mang lại cảm hứng mới.
Ví dụ minh họa chi tiết
Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình lập phương có cạnh là 3cm.
Phương pháp: Áp dụng trực tiếp các công thức đã học.
Giải:
- Diện tích một mặt của hình lập phương là:
3 x 3 = 9 (cm²) - Diện tích xung quanh của hình lập phương là:
9 x 4 = 36 (cm²) - Diện tích toàn phần của hình lập phương đó là:
9 x 6 = 54 (cm²)
Đáp số:
- Diện tích xung quanh: 36 cm²
- Diện tích toàn phần: 54 cm²
Đây là một ví dụ cơ bản giúp bạn dễ dàng hình dung và áp dụng công thức. Để mở rộng kiến thức, bạn có thể tìm hiểu thêm về các tác phẩm văn học cổ điển như tản viên từ phán sự lục, nơi các tri thức được gói gọn trong những câu chuyện sâu sắc.
Giới Thiệu Khái Niệm Thể Tích Của Một Hình
Ngoài diện tích, khái niệm thể tích cũng rất quan trọng trong hình học không gian, đặc biệt khi so sánh kích thước không gian mà các vật thể chiếm giữ.
Ví dụ 1: So sánh thể tích
Khi một hình lập phương nằm hoàn toàn bên trong một hình hộp chữ nhật, chúng ta có thể kết luận rằng thể tích của hình lập phương nhỏ hơn thể tích của hình hộp chữ nhật. Điều ngược lại cũng đúng: thể tích hình hộp chữ nhật lớn hơn thể tích hình lập phương.
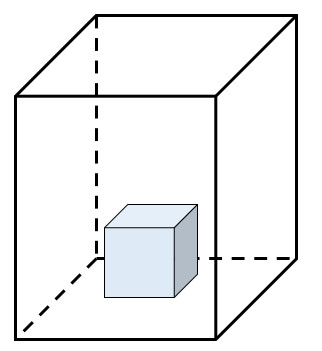So sánh thể tích hình lập phương nằm gọn trong hình hộp chữ nhật
Ví dụ 2: Thể tích bằng nhau
Nếu hình C được tạo thành từ 4 hình lập phương nhỏ giống nhau, và hình D cũng được tạo thành từ 4 hình lập phương nhỏ tương tự, thì chúng ta có thể khẳng định rằng thể tích hình C bằng thể tích hình D.
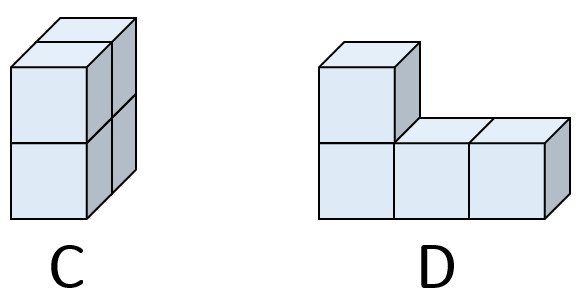Hai khối hình C và D minh họa khái niệm thể tích bằng nhau
Trong kỷ nguyên số, việc quản lý nội dung cũng đòi hỏi những kỹ năng nhất định, ví dụ như cách how to remove capcut watermark để có được những video chuyên nghiệp hơn.
Ví dụ 3: Thể tích tổng hợp
Xét hình P gồm 6 hình lập phương nhỏ như nhau. Khi ta tách hình P thành hai hình M và N, trong đó hình M có 4 hình lập phương và hình N có 2 hình lập phương, thì thể tích hình P chính là tổng thể tích của hình M và hình N.
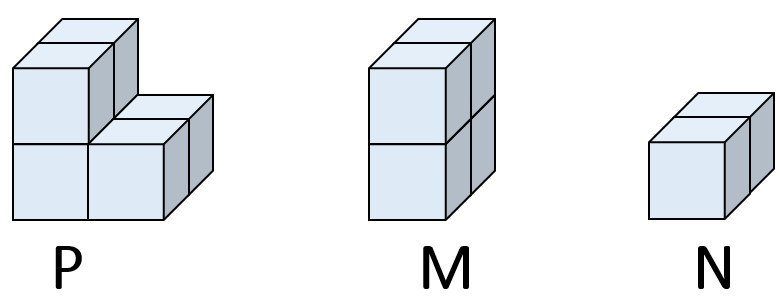Hình P chia thành M và N, minh họa tổng thể tích
Điều này cho thấy thể tích có tính chất cộng gộp. Sự hòa quyện của các yếu tố nhỏ để tạo nên một tổng thể lớn đôi khi gợi nhớ đến cách tình yêu là những ánh sáng lấp lánh của những khoảnh khắc đẹp.
Kết Luận
Nắm vững khái niệm và công thức tính diện tích toàn phần của hình lập phương là một kỹ năng toán học cơ bản nhưng vô cùng quan trọng, có thể ứng dụng trong nhiều tình huống thực tế. Từ việc ước tính lượng sơn cần dùng cho một chiếc hộp đến việc tính toán vật liệu xây dựng, kiến thức này đều hữu ích. Hy vọng qua bài viết này, bạn đã có cái nhìn rõ ràng hơn về hình lập phương, cách tính diện tích xung quanh, diện tích toàn phần của hình lập phương, và cả những khái niệm cơ bản về thể tích. Hãy tiếp tục luyện tập và khám phá thêm về thế giới hình học để ứng dụng vào cuộc sống một cách hiệu quả nhất!